大家好,我借鉴这位同学的代码(Homework0: weakly-compressible SPH) 试着写了下WCSPH,尽管我在调试期间找到很多错误, 但是我的模拟当前跑出来的结果还是非常的奇怪,能不能烦请各位看一看我的这个step() 函数是不是有什么理解上的错误。代码很短(20行),我用的是最暴力的算法,没做任何优化,其中的4个for循环分别对应下面的一组公式:
1).get density 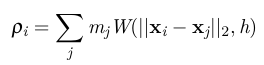
2).get pressure from density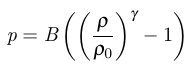
3). get change in pressure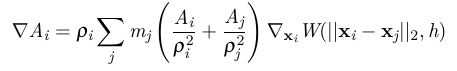
4). propagate dynamics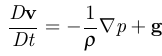
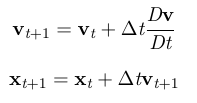
@ti.kernel
def step(self):
#1).get density
for p_i in self.positions:
self.density[p_i][0] = 0
for p_j in range(self.num_particles):
if p_i == p_j: continue
r = self.positions[p_i] - self.positions[p_j]
r_ij = r.norm()
self.density[p_i][0] += self.mass * self.cubic_kernel(r_ij, self.h)
#2).get pressure from density
for p_i in self.positions:
self.pressure[p_i][0] = self.pressure_equation_of_state(p_i)
#3). get change in pressure
for p_i in self.positions:
self.d_pressure[p_i] = [0, 0]
for p_j in range(self.num_particles):
if p_i == p_j: continue
r = self.positions[p_i] - self.positions[p_j]
r_ij = r.norm()
self.d_pressure[p_i] += self.mass * (self.pressure[p_i][0] / self.density[p_i][0]**2 + self.pressure[p_j][0] / self.density[p_j][0] ** 2) * self.cubic_kernel_derivative(r_ij, self.h) * r/r_ij
self.d_pressure[p_i] *= self.density[p_i][0]
#4). propagate dynamics
for p_i in self.positions:
self.velocities[p_i] += self.dt * ( self.d_pressure[p_i] * (-1/self.density[p_i][0]) + self.g)
self.positions[p_i] += self.dt * self.velocities[p_i]
在此先提前谢谢各位的帮助。
完整版的代码如下,运行就可以看到当前的模拟效果。
import numpy as np
import matplotlib.pyplot as plt
import time
from itertools import count, product
import taichi as ti
ti.init(arch=ti.cpu)
RIGHT = TOP = 0.95
LEFT = BOTTOM = 0.05
# PARTICAL_SIZE = 0.01
PARTICAL_SIZE = 0.1
DIM = 1000
#particle_start_positions = np.array(list(product(np.arange(LEFT + PARTICAL_SIZE, RIGHT, PARTICAL_SIZE), np.arange(0.5, 0.7, PARTICAL_SIZE))))
particle_start_positions = np.array([[0.2,0.3], [0.3,0.3]])
# particle_start_positions = np.array([[0.7,0.7]])
num_particles = len(particle_start_positions)
@ti.data_oriented
class WCSPH():
def __init__(self, particle_start_positions, dim = 2,
top = TOP, bottom = BOTTOM, left = LEFT, right = RIGHT):
self.dim = dim
self.num_particles = len(particle_start_positions)
self.particle_start_positions = particle_start_positions
self.positions = ti.Vector(self.dim, dt = ti.f32)
self.velocities = ti.Vector(self.dim, dt = ti.f32)
self.density = ti.Vector(1, dt = ti.f32)
self.pressure = ti.Vector(1, dt = ti.f32)
self.d_pressure = ti.Vector(self.dim, dt = ti.f32)
# this allows to give many vector/matrix the right shape at one go, rather than specifying shape per vector/matrix
ti.root.dense(ti.i, self.num_particles).place(self.positions, self.velocities, self.density, self.pressure, self.d_pressure)
self.positions.from_numpy(self.particle_start_positions)
self.dt = 1e-3
self.mass = 1.0
self.h = 1
self.g = ti.Vector([0, -9.0])
self.left_bound = left
self.right_bound = right
self.top_bound = top
self.bottom_bound = bottom
# @ti.kernel
# def initialise(self):
# for i in range(self.num_particles):
# self.positions[i] = self.particle_start_positions[i]
@ti.func
def pressure_equation_of_state(self, p_i, rho_0=1, gamma=7.0, c_0=20.0):
# Weakly compressible, tait function
b = rho_0 * c_0 ** 2 / gamma
return b * ((self.density[p_i][0] / rho_0) ** gamma - 1.0)
@ti.kernel
def step(self):
for p_i in self.positions:
self.density[p_i][0] = 0
for p_j in range(self.num_particles):
if p_i == p_j: continue
r = self.positions[p_i] - self.positions[p_j]
r_ij = r.norm()
self.density[p_i][0] += self.mass * self.cubic_kernel(r_ij, self.h)
for p_i in self.positions:
self.pressure[p_i][0] = self.pressure_equation_of_state(p_i)
for p_i in self.positions:
self.d_pressure[p_i] = [0, 0]
for p_j in range(self.num_particles):
if p_i == p_j: continue
r = self.positions[p_i] - self.positions[p_j]
r_ij = r.norm()
self.d_pressure[p_i] += self.mass * (self.pressure[p_i][0] / self.density[p_i][0]**2 + self.pressure[p_j][0] / self.density[p_j][0] ** 2) * self.cubic_kernel_derivative(r_ij, self.h) * r/r_ij
self.d_pressure[p_i] *= self.density[p_i][0]
for p_i in self.positions:
self.velocities[p_i] += self.dt * ( self.d_pressure[p_i] * (-1/self.density[p_i][0]) + self.g)
# self.velocities[p_i] += self.g
self.positions[p_i] += self.dt * self.velocities[p_i]
@ti.func
def simualteCollisions(self, p_i, vec, d):
# Collision factor, assume roughly 50% velocity loss after collision, i.e. m_f /(m_f + m_b)
c_f = 0.5
self.positions[p_i] += vec * d
self.velocities[p_i] -= (1.0+c_f) * self.velocities[p_i].dot(vec) * vec
@ti.kernel
def enforce_boundary(self):
for p_i in self.positions:
pos = self.positions[p_i]
if pos[0] < self.left_bound:
self.simualteCollisions(p_i, ti.Vector([1.0, 0.0]), self.left_bound - pos[0])
if pos[0] > self.right_bound:
self.simualteCollisions(p_i, ti.Vector([-1.0, 0.0]), pos[0] - self.right_bound)
if pos[1] > self.top_bound:
self.simualteCollisions(p_i, ti.Vector([0.0, -1.0]), pos[1] - self.top_bound)
if pos[1] < self.bottom_bound:
self.simualteCollisions(p_i, ti.Vector([0.0, 1.0]), self.bottom_bound - pos[1])
@ti.func
def update_density(self, i, j, r_ij):
self.density[i][0] += self.mass * self.cubic_kernel(r_ij, self.h)
@ti.func
def cubic_kernel(self, r, h):
# value of cubic spline smoothing kernel
k = 10. / (7. * np.pi * h ** 2)
q = r / h
assert q >= 0.0
res = ti.cast(0.0, ti.f32)
if q <= 1.0:
res = k * (1 - 1.5 * q ** 2 + 0.75 * q ** 3)
elif q < 2.0:
res = k * 0.25 * (2 - q) ** 3
return res
@ti.func
def cubic_kernel_derivative(self, r, h):
# derivative of cubcic spline smoothing kernel
k = 10. / (7. * np.pi * h ** 2)
q = r / h
assert q > 0.0
res = ti.cast(0.0, ti.f32)
if q < 1.0:
res = (k / h) * (-3 * q + 2.25 * q ** 2)
elif q < 2.0:
res = -0.75 * (k / h) * (2 - q) ** 2
return res
def main():
gui = ti.GUI("WCSPH", (DIM, DIM))
tmp = WCSPH(particle_start_positions)
# tmp.initialise()
while True:
#box
print("positions: ", tmp.positions)
print("velocities: ", tmp.velocities)
print("pressure: ", tmp.pressure)
print("d_pressure: ", tmp.d_pressure)
print("density: ", tmp.density)
print()
tmp.step()
tmp.enforce_boundary()
gui.line(begin=(LEFT, BOTTOM), end=(RIGHT, BOTTOM), color=0xFFFFFF, radius=1)
gui.line(begin=(LEFT, TOP), end=(RIGHT, TOP), color=0xFFFFFF, radius=1)
gui.line(begin=(LEFT, TOP), end=(LEFT, BOTTOM), color=0xFFFFFF, radius=1)
gui.line(begin=(RIGHT, TOP), end=(RIGHT, BOTTOM), color=0xFFFFFF, radius=1)
gui.circles(tmp.positions.to_numpy(), color = 0xFFFFFF, radius = PARTICAL_SIZE * DIM / 2)
gui.show()
if __name__ == '__main__':
main()