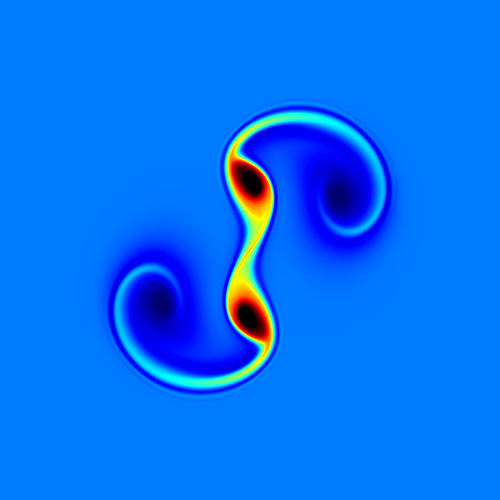
vortex method这类方法基于旋度形式的NS方程,适合模拟vortex ring之类的旋涡高度集中的现象。以及和stream function结合可以很好地保证divergence-free。SIGGRAPH 2015有一篇有趣的paper,A Stream Function Solver for Liquid Simulations,用的stream function模拟multiphase,不久前作者终于开源了,https://github.com/ryichando/shiokaze。
这里的Demo是以前用cpp写的一个2D测试改的,taichi用cpu后端要比写原生cpp慢一些,但是gpu后端就快多了,基于grid的计算性能还是可以的。stream function solver是最快的;vortex-in-cell solver慢一些,可能和实现有关,解了两次scalar poisson;Biot-Savart solver就慢多了,用vortex particles+fast multiple还是可以的,这里直接range遍历了。
import taichi as ti
import math
# ti.init(arch=ti.cpu)
ti.init(arch=ti.gpu)
N = 512
Nx = N
Ny = N
nTotal = Nx * Ny
dx = 1.0 / N
dt = 0.2 / N
ux = ti.var(dt=ti.f32, shape=(Nx, Ny)) # velocity x
uy = ti.var(dt=ti.f32, shape=(Nx, Ny)) # velocity y
omega = ti.var(dt=ti.f32, shape=(Nx, Ny)) # vorticity
omega_temp = ti.var(dt=ti.f32, shape=(Nx, Ny)) # vorticity
sigma = ti.var(dt=ti.f32, shape=(Nx, Ny)) # stream function
color_buffer = ti.Vector(3, dt=ti.f32, shape=(Nx, Ny))
solver_type = 0 # 0: stream func sovler, 1: vortex in cell solver, 2: biot-savart solver
solver_names = ["stream function solver",
"vortex-in-cell solver", "Biot-Savart solver"]
class ColorMap:
def __init__(self, h, wl, wr, c):
self.h = h
self.wl = wl
self.wr = wr
self.c = c
@ti.func
def clamp(self, x):
return max(0.0, min(1.0, x))
@ti.func
def map(self, x):
w = 0.0
if x < self.c:
w = self.wl
else:
w = self.wr
return self.clamp((w-abs(self.clamp(x)-self.c))/w*self.h)
jetR = ColorMap(1.5, .37, .37, .75)
jetG = ColorMap(1.5, .37, .37, .5)
jetB = ColorMap(1.5, .37, .37, .25)
@ti.func
def color_map(c):
return ti.Vector([jetR.map(c),
jetG.map(c),
jetB.map(c)])
@ti.kernel
def fill_velocity():
for i, j in ux:
_ux = ux[i, j]
_uy = uy[i, j]
color_buffer[i, j] = color_map(ti.sqrt(_ux * _ux + _uy * _uy))
@ti.kernel
def fill_vorticity():
for i, j in omega:
c = omega[i, j]
c = 0.25 + c * 0.01
color_buffer[i, j] = color_map(c)
@ti.kernel
def fill_streamfunc():
for i, j in sigma:
c = sigma[i, j] * 5.0 + 0.5
color_buffer[i, j] = color_map(c)
# -------------------------------------
def swap_buffers(a, b):
a, b = b, a
@ti.kernel
def copy_buffer(dst: ti.template(), src: ti.template()):
for i, j in src:
dst[i, j] = src[i, j]
# [-0.5, 0.5]
@ti.func
def xCoord(i):
return ((i + 0.5) / Nx) - 0.5
# [-0.5, 0.5]
@ti.func
def yCoord(j):
return ((j + 0.5) / Ny) - 0.5
@ti.func
def ix(i, j):
return i + j * Nx
@ti.func
def mod(a, b):
return int(a % b)
@ti.func
def sq(x):
return x ** 2
@ti.kernel
def initialize_vortices():
for i, j in ux:
s = 0.16
x = xCoord(i) * 2.0
y = yCoord(j) * 2.0
x0 = x - s
x1 = x + s
ux_ = 0.0
uy_ = 0.0
# add vortex
rr1 = sq(x0) + sq(y)
ux_ += - y * ti.exp(- rr1 / (2.0 * sq(0.12))) * 25.0
uy_ += x0 * ti.exp(- rr1 / (2.0 * sq(0.12))) * 25.0
# add vortex
rr2 = sq(x1) + sq(y)
ux_ += - y * ti.exp(- rr2 / (2.0 * sq(0.12))) * 25.0
uy_ += x1 * ti.exp(- rr2 / (2.0 * sq(0.12))) * 25.0
ux[i, j] = ux_
uy[i, j] = uy_
for i, j in omega:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
omega[i, j] = \
(uy[i_p, j] - uy[i_n, j]) / (2.0 * dx) \
- (ux[i, j_p] - ux[i, j_n]) / (2.0 * dx)
# solve L*x=-rhs using periodic boundary
# using red-black ordering for successive over-relaxation/Gauss-Seidel linear solver
@ti.kernel
def linear_solver_step(SOR_factor: ti.f32, mask: ti.template(),
x: ti.template(), rhs: ti.template()):
for i, j in x:
if mod(i + j, 2) == mask:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
x_update = (
- rhs[i, j] * sq(dx)
- x[i_p, j]
- x[i_n, j]
- x[i, j_p]
- x[i, j_n]) * -0.25
x[i, j] = SOR_factor * x_update + (1.0 - SOR_factor) * x[i, j]
@ti.kernel
def fix_streamfunc():
# since velocity is the gradient of sigma (the stream function),
# the constant drift in sigma is harmless to velocity,
# and the field is eased for better visualization
sigmaMean = 0.0
for i, j in sigma:
sigmaMean += sigma[i, j]
sigmaMean /= nTotal
for i, j in sigma:
sigma[i, j] -= sigmaMean
def poisson_solver(num_iterations, x, rhs):
SOR_factor = 1.99 # 1.0 for Gauss-Seidel
for iters in range(num_iterations):
linear_solver_step(SOR_factor, iters % 2, x, rhs)
def solve_streamfunc(num_iterations):
# solve L*sigma=-omega using periodic boundary
poisson_solver(num_iterations, sigma, omega)
fix_streamfunc()
@ti.kernel
def reconstruct_velocity_sigma():
# u = curl(sigma)
# in 2D, u = grad x (0,0,sigma) = (par_y_sigma, -par_x_sigma, 0)
for i, j in sigma:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
ux[i, j] = (sigma[i, j_p] - sigma[i, j_n]) / (2.0 * dx) # par_y_sigma
uy[i, j] = - (sigma[i_p, j] - sigma[i_n, j]) / \
(2.0 * dx) # -par_x_sigma
# approximate Biot-Savart law, slow
# using the 2D version of the Biot-Savart equation
@ti.kernel
def reconstruct_velocity_biot_savart():
radius = 100
patch_size = 4
num_patches = radius // patch_size
d_patch_size = patch_size * patch_size * sq(dx)
for i, j in omega:
ux_ = 0.0
uy_ = 0.0
for m_, n_ in ti.ndrange((-num_patches, num_patches + 1),
(-num_patches, num_patches + 1)):
m = m_ * patch_size
n = n_ * patch_size
if (m != 0 or n != 0):
ii = mod(i + m + Nx, Nx)
jj = mod(j + n + Ny, Ny)
vorticity = omega[ii, jj]
# x - p
dist_x = - m * dx
dist_y = - n * dx
# omega \cross (x - p)
vx = vorticity * - dist_y
vy = vorticity * dist_x
rr = (dist_x * dist_x + dist_y * dist_y)
ux_ += vx / rr
uy_ += vy / rr
ux[i, j] = ux_ / (2.0 * math.pi) * d_patch_size
uy[i, j] = uy_ / (2.0 * math.pi) * d_patch_size
# vortex in cell method
# solve L*U=-curl(omega)
@ti.kernel
def compute_omega_curl_x(temp: ti.template()):
for i, j in omega:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
temp[i, j] = (omega[i, j_p] - omega[i, j_n]) / \
(2.0 * dx) # par_y_omega
@ti.kernel
def compute_omega_curl_y(temp: ti.template()):
for i, j in omega:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
sigma[i, j] = - (omega[i_p, j] - omega[i_n, j]) / \
(2.0 * dx) # -par_x_omega
def reconstruct_velocity_vic():
compute_omega_curl_x(sigma)
poisson_solver(20, ux, sigma)
compute_omega_curl_y(sigma)
poisson_solver(20, uy, sigma)
@ti.kernel
def advect_vorticity(dt_substep: ti.f32):
# advection of omega by 2nd order upwind scheme
for i, j in omega:
i_p = mod(i + 1, Nx)
i_n = mod(i - 1 + Nx, Nx)
j_p = mod(j + 1, Ny)
j_n = mod(j - 1 + Ny, Ny)
i_p2 = mod(i + 2, Nx)
i_n2 = mod(i - 2 + Nx, Nx)
j_p2 = mod(j + 2, Ny)
j_n2 = mod(j - 2 + Ny, Ny)
ux_pos = max(ux[i, j], 0.0)
ux_neg = min(ux[i, j], 0.0)
uy_pos = max(uy[i, j], 0.0)
uy_neg = min(uy[i, j], 0.0)
# second order
omega_dx_pos = \
(- omega[i_p2, j] + 4.0 * omega[i_p, j] -
3.0 * omega[i, j]) / (2.0 * dx)
omega_dx_neg = \
(omega[i_n2, j] - 4.0 * omega[i_n, j] +
3.0 * omega[i, j]) / (2.0 * dx)
omega_dy_pos = \
(- omega[i, j_p2] + 4.0 * omega[i, j_p] -
3.0 * omega[i, j]) / (2.0 * dx)
omega_dy_neg = \
(omega[i, j_n2] - 4.0 * omega[i, j_n] +
3.0 * omega[i, j]) / (2.0 * dx)
omega_temp[i, j] = omega[i, j] - dt_substep * (
ux_pos * omega_dx_neg + ux_neg * omega_dx_pos +
uy_pos * omega_dy_neg + uy_neg * omega_dy_pos)
def solve_velocity_streamfunc():
solve_streamfunc(20)
reconstruct_velocity_sigma()
def solve_velocity_vic():
reconstruct_velocity_vic()
def solve_biot_savart():
reconstruct_velocity_biot_savart()
def initialize():
initialize_vortices()
solve_streamfunc(1000)
def run_iteration():
num_substeps = 5 # to deal with large CFL
dt_substep = dt / num_substeps
for iters in range(num_substeps):
advect_vorticity(dt_substep)
# may use the swap style in the stable-fluids example
copy_buffer(omega, omega_temp)
if (solver_type == 0):
solve_velocity_streamfunc()
elif (solver_type == 1):
solve_velocity_vic()
else:
solve_biot_savart()
def toggle_solver():
global solver_type
solver_type = (solver_type + 1) % 3
if (solver_type == 0):
sigma.fill(0.0)
class Viewer:
def __init__(self, dump):
self.display_mode = 0
self.is_active = True
self.dump = dump
self.frame = 0
if self.dump:
result_dir = "./results"
self.video_manager = ti.VideoManager(
output_dir=result_dir, framerate=24, automatic_build=False)
def toggle(self):
self.display_mode = (self.display_mode + 1) % 3
def active(self):
return self.is_active
def draw(self, gui):
if self.display_mode == 0:
fill_vorticity()
display_name = "vorticity"
elif self.display_mode == 1:
fill_velocity()
display_name = "velocity"
else:
fill_streamfunc()
display_name = "stream function"
img = color_buffer.to_numpy()
gui.set_image(img)
gui.text(content=f"display: {display_name}",
pos=(0.0, 0.99), color=0xFFFFFF)
if self.dump:
self.video_manager.write_frame(img)
print(f"\rframe {self.frame} written", end="")
self.frame = self.frame + 1
if self.frame == 300:
self.video_manager.make_video(gif=True, mp4=True)
self.is_active = False
def main():
initialize()
viewer = Viewer(False)
gui = ti.GUI("vortex method", Nx, Ny)
while viewer.active():
for e in gui.get_events(ti.GUI.PRESS):
if e.key == ti.GUI.ESCAPE or e.key == 'q':
exit(0)
elif e.key == 'r':
initialize()
elif e.key == ' ':
viewer.toggle()
elif e.key == 's':
toggle_solver()
for iters in range(10):
run_iteration()
viewer.draw(gui)
gui.text(content=f"solver: {solver_names[solver_type]}",
pos=(0, 0.96), color=0xFFFFFF)
gui.text(content="r: reset simulation", pos=(0, 0.86), color=0xFFFFFF)
gui.text(content="q, esc: quit", pos=(0, 0.83), color=0xFFFFFF)
gui.text(content="space: toggle display mode",
pos=(0, 0.8), color=0xFFFFFF)
gui.show()
if __name__ == '__main__':
main()