对于公式:
C_p^{n+1} = \frac 4 {{\Delta x}^2} \sum_i w_{ip} \mathbf{v}_i^{n+1}{\left(x_i - x_p^n\right)}^T
第一个问题:4/dx^2
GAMES201似乎并没有讲这个 \frac 4 {{\Delta x}^2} 如何推出来的,只说了MPM中这一项是从APIC里用Quadratic得来的,但是在上一讲APIC时也没有推导这一项
在APIC论文原文中,C矩阵是两个矩阵计算得出的:
C_p^n=B_p^n(D_p^n)^{-1} \\
D_p^n=\sum_i w_{ip}^n{\left(x_i - x_p^n\right)} {\left(x_i - x_p^n\right)}^T \\
B_p^{n+1}=\sum_i w_{ip}^n \tilde{\mathbf{v}}_i^{n+1} {\left(x_i - x_p^n\right)}^T
论文在后面又说在Quadratic差值形式下很简单可以化为 D_p^n = \frac 1 4 \Delta x^2 I , 从而得出GAMES201中计算 C_p^{n+1} 的形式。但是论文原文也没有说如何推出这个 \frac 1 4 \Delta x^2 I
我试了两整天也没办法把这个 \frac 1 4 \Delta x^2 I 推出来
问题2:张量积
APIC论文原文中提到使用 v(x) = v_p + C_p(x - x_p) 来近似估计粒子p邻域的速度场,并且GAMES201中也使用了一张直观的图片来解释 C_p 矩阵。
照这样看 C_p 矩阵应该类似于速度关于位置的导数关系, 在应用中应该使用解线性方程 v(x) = v_p + C_p(x - x_p) 的方式来求解 C_p
但是实际上,应用中使用了张量积来近似这个导数关系,并且通过除以 \Delta x^2 来解决了量纲对不上的问题。这非常的奇怪
以上两个问题,希望有高人解答
atdp
#2
太极萌新在此,遇到了同样的问题,试着推了一下:
Siggraph 2016 的课里提到了Quadratic和Cubic Spline的定义
(1)
然后第一个公式 \sum_i 要加三个维度的格点, w_{ip} 也是三个方向上的 N(x) 相乘。
可以根据 D^n_p 定义,逐元素算这个求和
(D^n_p)_{kl} = \sum_i w_{ip}^n (x_i-x_p^n)_k(x_i-x_p^n)_l=\sum_i N(t_{ix})N(t_{iy})N(t_{iz})(x_i-x_p^n)_k(x_i-x_p^n)_l
其中 \displaystyle t_{ix}=\left(\frac{x_i-x^n_p}{\Delta x}\right)_x , N(t_{ix}) 就是 x 方向的权重
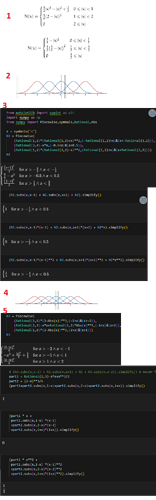
如果用Quadratic spline, 一个维度上只需要考虑3个最近的格点,因为 |x|>1.5 权重是0,如图所示
三维一共加27个点
(2)
现在关键的来了,这三个权重的和 \sum_i w_i 竟然是1, \sum_i w_i t_i’=0 , \sum_i w_i t_i'^2=1/4 , 为什么我也不知道,可能B-Spline的奇妙特性吧
有图为证:
(3)
然后上面的求和就能算了,可以考虑几种情况,比如 k,l=x,y ,然后先沿着 z 求和这样两个 (x_i-x_p^n) 项可以先提出来之类的。 反正怪麻烦的,因为 \sum_i 其实是 \sum_x\sum_y\sum_z ,但是最后能算出来 D 确实是对角的。完整过程在此
Cubic spline类似,但是每个维度要加4个而不是3个权重:
(4)
类似地,
(5)
过于复杂甚至把sympy卡死了,只能手动输…
不过这个问题太坑了,究竟是谁想到spline这么奇怪的性质?也有可能真相特别简单,被我给想复杂了…
至于张量积,我还没看p2g和g2p完整的推导,所以没看懂问题。不过 C_p 的式子数学上成立不就行了? 除 \Delta x^2 是因为除 D^n_p, D^n_p=\frac{(\Delta x)^2}{4} I ,就是按公式来的?
1 个赞
非常感谢,这个式子 \sum_i w_i t_i'^2=1/4 对我很有启发,我试着从这里继续推导以下P2G和G2P,看能不能有个更直观简洁的解释
对于张量积的问题,我先在有些思路:
我们的确想用 C_p 来表示速度关于位置的导数关系,但直接解方程确实过于复杂,考虑做一些变形
对于一个离 x_p 很近的位置 x 以及他们的速度 v(x) ,我们想要求得一个3x3雅可比矩阵
C_p = \frac {\partial v} {\partial x}
直接算不方便,但由于我们可以合理利用粒子-网格之间的关系权重 w_{ip} 作为中介:
C_p = \frac {\partial v} {\partial w} \cdot \frac {\partial w} {\partial x}
由于我们在G2P时有 v_p \approx \sum_i w_{ip} v_i , 则可以认为 \frac {\partial v} {\partial w} \approx v_i
则
C_p = \sum_i v_i \cdot \frac {\partial w} {\partial x} = \sum_i v_i (\nabla w_{ip})^T
这个式子也与Siggraph 2016中第42页相同。如何求得 \nabla w_{ip} 我暂时还没有推导完,这里写一下思路:
由B-Spline的性质可以得到 \sum_i w_{ip} = 1 (感谢atdp提醒,已更正), 以及:
\sum_i w_{ip} (x_i - x_p) = 0
等式两边对 x_p 微分得到 (推导已经过更正)
\sum_i (x_i - x_p) (\nabla w_{ip})^T + \sum_i w_{ip} \nabla (x_i - x_p) = 0 \\
\sum_i (x_i - x_p) (\nabla w_{ip})^T - \sum_i w_{ip} \cdot I= 0 \\
\sum_i (x_i - x_p) (\nabla w_{ip})^T = I
应该有办法基于这些结论把 \nabla w_{ip} 整出来,最后结果确实是算法的张量积形式
atdp
#6
之前还真没注意这个问题,因为我看这篇APIC的文章里是把 C_p=\nabla v 当前提条件的。
然后 Siggraph 2016 也没说它们相等,画了一下图,quadratic spline的情况好像确实不相等,但是比较接近
(一个是 C_p = \frac{4}{\Delta x^2}\sum_i w_{ip} v_i^{n+1}(x_i-x_p^n)^T , 另一个是 C_p=\sum_i v_i(\nabla w_{ip})^T, 可以画 w_{ip}(x_i-x_p^n)^T 和 (\nabla w_{ip})^T 比较一下)
MLS-MPM的文章的公式17倒是提了一下,但没细说
现在有种管中窥豹的感觉,似乎除了把论文都读一遍外没其他办法了。由于时间原因,我选择放弃并且相信论文 >_<
另提一下 \sum_i w_{ip}=1\neq0 ,此事在[这里](An angular momentum conserving affine-particle-in-cell method)(为什么只让我放两个链接)亦有记载(公式16),当时没看到。唉,亏我想了这么久…
但无论如何MPM还是很酷炫的,像是网格上的SPH,效果还这么好,令我大开眼界。感谢胡老师,以后有机会补票吧
我解不出来 \nabla w_{ip} 是什么,但是APIC第6页5.3节最后一段给出了答案: \nabla w_{ip}=w_{ip} (D_p)^{-1} (x_i-x_p)
我可以接着之前的推导验证这个答案:
\sum_i (x_i - x_p) (\nabla w_{ip})^T = I \\
\sum_i \nabla w_{ip} (x_i - x_p)^T = I \\
\sum_i w_{ip} (D_p)^{-1} (x_i-x_p) (x_i - x_p)^T \\
=(D_p)^{-1} \sum_i w_{ip} (x_i-x_p) (x_i - x_p)^T \\
=(D_p)^{-1} D_p = I
看起来应该是正确的
至此,我们应该能够完全推导出 C_p = B_p (D_p)^{-1} ,感谢atdp的帮助
借助DeepSeek和你的详细推导,我逐渐理解了 D_p 为什么是对角的常量
\begin{align}
D_p &= \sum_i w_{ip} (x_i - x_p)(x_i-x_p)^T \\
&= \sum_i w_{ip} x_i \cdot x_i^T - \sum_i w_{ip} x_i \cdot x_p^T - \sum_i w_{ip} x_p \cdot x_i^T + \sum_i w_{ip} x_p \cdot x_p^T \\
&= \left( \sum_i w_{ip} x_i \cdot x_i^T \right) - x_p \cdot x_p^T \\
&= \left( \sum_i w_{ip} x_i \cdot x_i^T \right) - \left(\sum_i w_{ip} x_i \right) \cdot \left(\sum_i w_{ip} x_i \right)^T
\end{align}
这其实代表了网格格点各个维度坐标的协方差
很显然,网格不同维度是正交的,不同维度之间对插值没有任何影响,所以 (D_p)_{kl} = 0 \ (k \neq l) , D_p 是对角的。
对角上的元素,由于B-Spline的稳定性,能够确保插值元素 (格点 x_i )的间距如果是恒定,那么方差也能保持恒定。按照atdp的推导,Quadratic的方差恒为1/4,Cubic的方差恒为1/3
atdp
#10
哇学到了,竟然还有向量版的协方差,并且 w_{ip} 起到了类似概率的作用
APIC第6页5.3节说的 \nabla w_{ip} 是trilinear interpolation,那我们确实用了某种近似