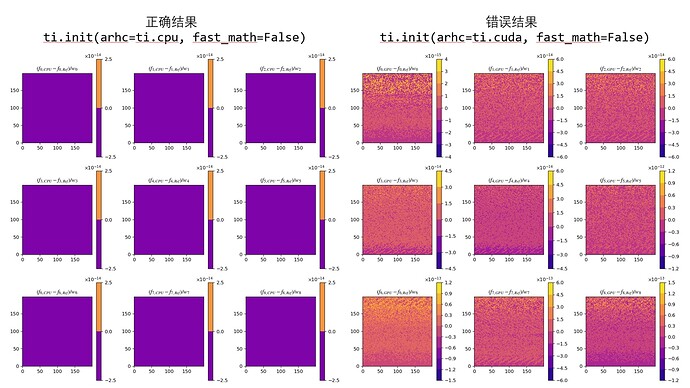
我是用 1.6 版本的 TaiChi 运行了下面的程序,但是 TaiChi 点乘后相加的行为似乎有平台差异,请问。
这是不同结构下的结果对比图:
这是测试代码:
import numpy as np
import taichi as ti
import matplotlib.pyplot as plt
plt.rcParams["axes.formatter.use_mathtext"] = True
plt.rcParams["mathtext.fontset"] = "stix"
# |=> Select arch
ARCH = "CPU"
if ARCH == "CPU": _TI_ARCH = ti.cpu
elif ARCH == "GPU": _TI_ARCH = ti.cuda
# |=> Initialize TaiChi
ti.init(arch=_TI_ARCH,default_fp=ti.f64,default_ip=ti.i32,fast_math=False)
# |=> Generate parameters
D, Q = 2, 9
c_np = np.array([[0, 0], [ 1, 0], [ 0, 1], [-1, 0], [0, -1],
[1, 1], [-1, 1], [-1, -1], [ 1, -1]], dtype=np.int32)
w_np = np.array([4/9, 1/9, 1/9, 1/9, 1/9, 1/36, 1/36, 1/36, 1/36], dtype=np.float64)
c = ti.Vector.field(n=D, dtype=ti.i32, shape=(9, ))
c.from_numpy(c_np)
w = ti.field(ti.f64, shape=(Q, ))
w.from_numpy(w_np)
# |=> Generate Test field
Nx, Ny = 200, 200
vel_np = np.arange(Nx*Ny*2).reshape(Nx, Ny, 2).astype(np.float64) / (Nx*Ny)
vel = ti.Vector.field(D, ti.f64, shape=(Nx, Ny))
vel.from_numpy(vel_np)
rho = ti.field(ti.f64, shape=(Nx, Ny))
rho.from_numpy(np.ones((Nx, Ny), dtype=np.float64))
feq = ti.Vector.field(Q, ti.f64, shape=(Nx, Ny))
# |=> TaiChi function for test
@ti.func
def compute_node_feq(i: int, j: int):
uu = ti.math.dot(vel[i, j], vel[i, j])
ti.loop_config(serialize=True)
for q in ti.ndrange(Q):
cu = ti.math.dot(c[q], vel[i, j])
feq[i, j][q] = 1.0 + 3.0*cu + 4.5 * ti.pow(cu, 2.0) - 1.5 * uu
return
# |=> TaiChi kernel for test
@ti.kernel
def compute_feq(Nx: int, Ny: int):
for i, j in ti.ndrange(Nx, Ny):
compute_node_feq(i, j)
return
if __name__ == "__main__":
# |=> Run TaiChi kernel code
compute_feq( Nx, Ny )
# |=> Answer computed by TaiChi
TI_feq = feq.to_numpy()
# |=> Exact answer
feq_ans = np.zeros((Nx, Ny, Q))
for q in range(Q):
cu = c_np[q, 0] * vel_np[:, :, 0] + c_np[q, 1] * vel_np[:, :, 1]
uv = vel_np[:, :, 0]**2 + vel_np[:, :, 1]**2
feq_ans[:, :, q] = 1.0 + 3.0*cu + 4.5*(cu**2) - 1.5*uv
# |=> Plot relative error: It should be zero theoreticaly!
# But the wrong happened.
plt.subplots(3, 3, figsize=(10, 10), dpi=120)
for idx, i in enumerate(range(9)):
plt.subplot(3, 3, idx+1)
plt.title(
"$(f_{} - f_{})/ w_{}$".format(
"{" + str(i) + f",{ARCH}" +"}",
"{" + str(i) + ",Ref" +"}",
i
)
)
tmp = (TI_feq[:,:,idx] - feq_ans[:,:,idx]) / w_np[idx]
plt.contourf(tmp, cmap="plasma")
plt.colorbar()
plt.axis("scaled")
pass
plt.tight_layout()
plt.show()