当矩阵是稀疏矩阵的时候,也就是矩阵99%以上的元素都为0的时候,应该用特殊的数据结构去存储矩阵以及计算矩阵与向量的乘法。
数据结构:CSR(compressed sparse row)
存储稀疏的数据结构一般用CSR格式。
CSR分三个数组存储。
data: 一维float数组,按照从左到右,从上到下,一个一个地记录非零元
indices: 一维int数组, 记录非零元的矩阵列下标。
indptr:一维int数组, 记录每行的首元素对应在data中的下标。
我们可以用scipy来设定一个稀疏矩阵A,然后乘以向量v,并作为我们的对照组。
A = scipy.sparse.csr_array((dat, ind, ptr))
res0 = A@v
算法:spmv
接下来,如何设计稀疏矩阵的算法呢?
实现
为了方便调试,我们先用python和numpy写一个小例子,然后再改写成taichi。改写非常容易。
# numpy 版本 用作演示
def spmv(dat, ind, ptr, v):
res = np.zeros((len(ptr)-1), dtype=np.float32)
dv = np.ones_like(ind, dtype=np.float32) #dat * v
v_ = np.zeros_like(ind, dtype=np.float32) #v[ind]
for i in range(len(ind)):
idx = ind[i]
v_[i] = v[idx]
dv[i] = v[idx] * dat[i]
for k in range(len(ptr)-1):
for j in range(ptr[k], ptr[k+1]):
res[k] += dv[j]
return res
def test_small_case():
# small case for tutorial
dat = np.array([1,2,3,4,5,6], dtype=np.float32)
ind = np.array([0,2,0,1,2,1], dtype=np.int32)
ptr = np.array([0,2,5], dtype=np.int32)
v = np.array([1,2,3], dtype=np.float32)
res0 = spmv(dat, ind, ptr, v)
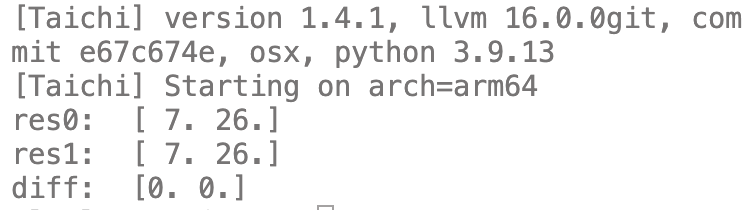
print("res0: ", res0)
A = sp.csr_array((dat, ind, ptr))
res1 = A@v
print("res1: ", res1)
diff = res0 - res1
print("diff: ", diff)
if __name__ == "__main__":
test_small_case() # small case for tutorial
其中,v_是step2中得到的数组;
dv就是step3中得到的数据
res是结果数组
运行结果:
然后,我们将其改写为taichi版本来提速。
@ti.kernel
def spmv_kernel( dat: ti.template(),
ind: ti.template(),
ptr: ti.template(),
v : ti.template(),
res: ti.template(),
dv : ti.template()):
for i in range(ind.shape[0]):
idx = ind[i]
dv[i] = v[idx] * dat[i]
for k in range(ptr.shape[0]-1):
for j in range(ptr[k], ptr[k+1]):
res[k] += dv[j]
def spmv_ti(dat, ind, ptr, v):
# t_start = time.time()
res_ti = ti.field(shape=(len(ptr)-1), dtype=ti.f32)
dv_ti = ti.field(shape=(len(ind)), dtype=ti.f32)
dat_ti = ti.field(shape=(len(ind)), dtype=ti.f32)
ind_ti = ti.field(shape=(len(ind)), dtype=ti.i32)
ptr_ti = ti.field(shape=(len(ptr)), dtype=ti.i32)
v_ti = ti.field(shape=(len(v)), dtype=ti.f32)
dat_ti.from_numpy(dat)
ind_ti.from_numpy(ind)
ptr_ti.from_numpy(ptr)
v_ti.from_numpy(v)
# print(f"field: {time.time()-t_start:.2g}s")
# t_before_kernel = time.time()
spmv_kernel(dat_ti, ind_ti, ptr_ti, v_ti, res_ti, dv_ti)
# t_after_kernel = time.time()
# print(f"kernel: {t_after_kernel-t_before_kernel:.2g}s")
ret = res_ti.to_numpy()
# print(f"to_numpy: {time.time()-t_after_kernel:.2g}s")
return ret
def test_large_case(N=1000):
A = sp.random(N, N, density=0.01, format='csr',dtype=np.float32)
dat = A.data
ind = A.indices
ptr = A.indptr
v = np.random.rand(N).astype(np.float32)
t0 = time.time()
A1 = sp.csr_matrix((dat, ind, ptr),dtype=np.float32)
res_scipy = A1@v
t1 = time.time()
res_mynp = spmv(dat, ind, ptr, v)
t2 = time.time()
res_myti = spmv_ti(dat, ind, ptr, v)
t3 = time.time()
t_scipy = t1 - t0
t_mynp = t2 - t1
t_myti = t3 - t2
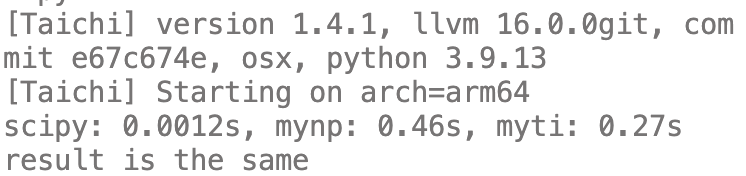
print(f"scipy: {t_scipy:.2g}s, mynp: {t_mynp:.2g}s, myti: {t_myti:.2g}s")
if np.allclose(res_scipy, res_myti, atol=1e-6, rtol=1e-3) and\
np.allclose(res_scipy, res_mynp, atol=1e-6, rtol=1e-3):
print("result is the same")
return True
else:
print("result is different")
res_scipy = A@v
res_mynp = spmv(dat, ind, ptr, v)
res_myti = spmv_ti(dat, ind, ptr, v)
return False
test_large_case(10000)
运行结果
可见,没有scipy快,但是肯定比python版本快一些。毕竟scipy的spmv是经过优化的,我们这个只是个小例子,不可能比人家快了。(另外说一句,taichi耗时最多的部分其实在创建field和从numpy转换数据)
对N=10000…20000,我测试了十组,都是这个结论。
结果如下
参考
【intro to parallel programming, NVIDIA GPU CUDA programming,GPU CUDA编程】 intro to parallel programming, NVIDIA GPU CUDA programming,GPU CUDA编程_哔哩哔哩_bilibili
sildes: 【金山文档】 2023-10-25 关于spmv CSR和Matrix-free
https://kdocs.cn/l/clW7ztNAdwaz
完整代码
'''
sparse matrix times vector for taichi
sparse matrix is given by csr(compressed sparse row) format
csr: the column indices for row i are stored in indices[indptr[i]:indptr[i+1]] and their corresponding values are stored in data[indptr[i]:indptr[i+1]].
See https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_array.html#scipy.sparse.csr_array
A.indptr (int array, size=nrows+1): ptr (ptr[0]=0, ptr[-1]=nnz)
A.indices(int array, size=nnz) : ind
A.data (float array, size=nnz) : dat
v (float array, size=ncols) : v
A = scipy.sparse.csr_array((dat, ind, ptr))
res0 = A@v # scipy
res1 = spmv(dat, ind, ptr, v) # numpy
res2 = spmv_ti(dat, ind, ptr, v)# taichi
sildes: 【金山文档】 2023-10-25 关于spmv CSR和Matrix-free
https://kdocs.cn/l/clW7ztNAdwaz
'''
import numpy as np
import scipy.sparse as sp
import taichi as ti
import time
ti.init(arch=ti.cpu)
def spmv(dat, ind, ptr, v):
res = np.zeros((len(ptr)-1), dtype=np.float32)
dv = np.ones_like(ind, dtype=np.float32) #dat * v
v_ = np.zeros_like(ind, dtype=np.float32) #v[ind]
for i in range(len(ind)):
idx = ind[i]
v_[i] = v[idx]
dv[i] = v[idx] * dat[i]
for k in range(len(ptr)-1):
for j in range(ptr[k], ptr[k+1]):
res[k] += dv[j]
return res
@ti.kernel
def spmv_kernel( dat: ti.template(),
ind: ti.template(),
ptr: ti.template(),
v : ti.template(),
res: ti.template(),
dv : ti.template()):
for i in range(ind.shape[0]):
idx = ind[i]
dv[i] = v[idx] * dat[i]
for k in range(ptr.shape[0]-1):
for j in range(ptr[k], ptr[k+1]):
res[k] += dv[j]
def spmv_ti(dat, ind, ptr, v):
# t_start = time.time()
res_ti = ti.field(shape=(len(ptr)-1), dtype=ti.f32)
dv_ti = ti.field(shape=(len(ind)), dtype=ti.f32)
dat_ti = ti.field(shape=(len(ind)), dtype=ti.f32)
ind_ti = ti.field(shape=(len(ind)), dtype=ti.i32)
ptr_ti = ti.field(shape=(len(ptr)), dtype=ti.i32)
v_ti = ti.field(shape=(len(v)), dtype=ti.f32)
dat_ti.from_numpy(dat)
ind_ti.from_numpy(ind)
ptr_ti.from_numpy(ptr)
v_ti.from_numpy(v)
# print(f"field: {time.time()-t_start:.2g}s")
# t_before_kernel = time.time()
spmv_kernel(dat_ti, ind_ti, ptr_ti, v_ti, res_ti, dv_ti)
# t_after_kernel = time.time()
# print(f"kernel: {t_after_kernel-t_before_kernel:.2g}s")
ret = res_ti.to_numpy()
# print(f"to_numpy: {time.time()-t_after_kernel:.2g}s")
return ret
def test_small_case():
# small case for tutorial
dat = np.array([1,2,3,4,5,6], dtype=np.float32)
ind = np.array([0,2,0,1,2,1], dtype=np.int32)
ptr = np.array([0,2,5], dtype=np.int32)
v = np.array([1,2,3], dtype=np.float32)
res0 = spmv(dat, ind, ptr, v)
print("res0: ", res0)
A = sp.csr_array((dat, ind, ptr))
res1 = A@v
print("res1: ", res1)
diff = res0 - res1
print("diff: ", diff)
def test_large_case(N=1000):
A = sp.random(N, N, density=0.01, format='csr',dtype=np.float32)
dat = A.data
ind = A.indices
ptr = A.indptr
v = np.random.rand(N).astype(np.float32)
t0 = time.time()
A1 = sp.csr_matrix((dat, ind, ptr),dtype=np.float32)
res_scipy = A1@v
t1 = time.time()
res_mynp = spmv(dat, ind, ptr, v)
t2 = time.time()
res_myti = spmv_ti(dat, ind, ptr, v)
t3 = time.time()
t_scipy = t1 - t0
t_mynp = t2 - t1
t_myti = t3 - t2
print(f"scipy: {t_scipy:.2g}s, mynp: {t_mynp:.2g}s, myti: {t_myti:.2g}s")
if np.allclose(res_scipy, res_myti, atol=1e-6, rtol=1e-3) and\
np.allclose(res_scipy, res_mynp, atol=1e-6, rtol=1e-3):
print("result is the same")
return True
else:
print("result is different")
res_scipy = A@v
res_mynp = spmv(dat, ind, ptr, v)
res_myti = spmv_ti(dat, ind, ptr, v)
return False
def test_different_N():
for _ in range(10):
N = np.random.randint(10000, 20000)
print(f"\ncase:{_}\tN: {N}")
suc = test_large_case(N)
if not suc:
exit()
if __name__ == "__main__":
# test_small_case() # small case for tutorial
test_different_N() # large case for performance test