Multigrid方法的核心思想就是不同频率的收敛速度是不同的。
让我们来用实验说明不同的频率对迭代法收敛速度的影响
本实验来自A Multigrid Tutotrial(ppt p.23)
Home Page for "A Multigrid Tutorial," 2nd edition
首先, 我们要求解的问题是
Au=0
离散形式为
-u_{i-1} + 2u_i - u_{i+1} = 0\\
1\leq i \leq N-1
边界值为
u_0 = u_{N} = 0
(我们用u代表真值,v代表近似解)
我们将Fourier modes作为初始值, 其中N=64, 即
\overrightarrow{v_k}=\left(v_i\right)_k=\sin \left(\frac{i k \pi}{N}\right)
1 \leq i \leq N-1, \quad
1 \leq k \leq N-1
其中i代表component, k代表mode
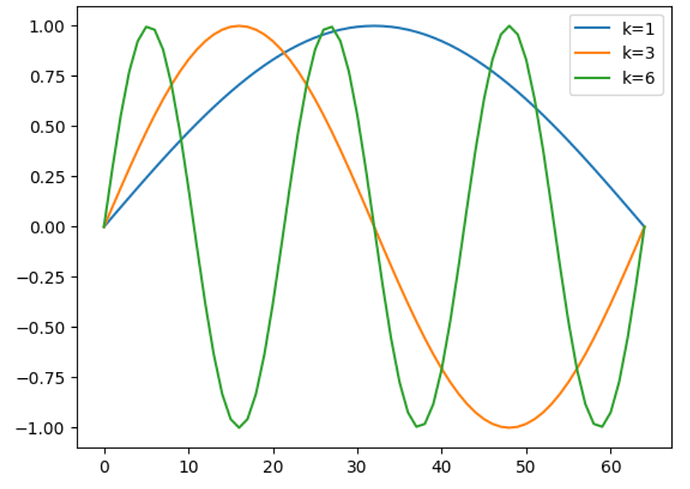
我们绘制出k=1,3,6的图像
import matplotlib.pyplot as plt
import numpy as np
N = 64
v = np.zeros((N+1,N+1),dtype=np.float64)
for i in range(1,N):
for k in range(1,N):
v[i,k] = np.sin(i*k*np.pi/N)
v1 = v[:,1]
v3 = v[:,2]
v6 = v[:,6]
plt.plot(v1, label="k=1")
plt.plot(v3, label="k=3")
plt.plot(v6, label="k=6")
plt.legend()
可见k=1,3,6频率越来越高。
可见k=1,3,6频率越来越高。
然后我们利用weighted Jacobi迭代法进行迭代, 其中omega=2/3
它的迭代公式为:
v_i^{(new)}=(1-\omega)v_{i}^{(old)} + (\omega/ 2) \left(v_{i-1}^{(old)}+v_{i+1}^{(old)} +h^2 f_i \right)
在我们的例子中,omega=2/3, f=0, h=1/N
我们设定初始值为
v_0=\frac{1}{3}\left(\sin \left(\frac{j \pi}{N}\right)+\sin \left(\frac{6 j \pi}{N}\right)+\sin \left(\frac{32 j \pi}{N}\right)\right)
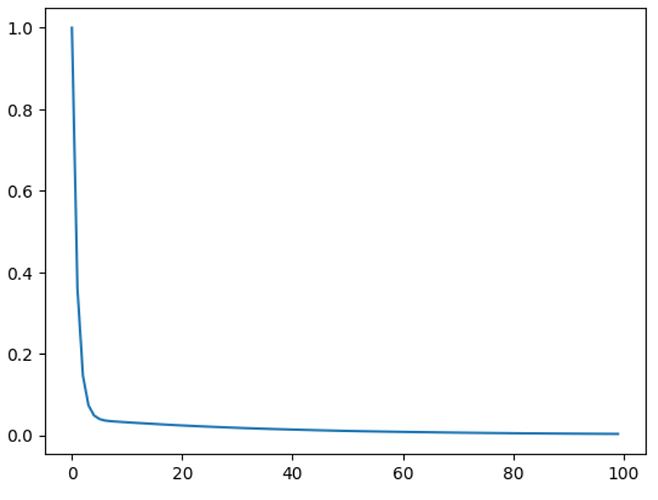
# 首先我们绘制v的误差下降曲线
v0 = np.zeros((N+1),dtype=np.float64)
for j in range(1,N):
v0[j] = 1/3 * (np.sin(j*np.pi/N) + np.sin(6*j*np.pi/N) + np.sin(32*j*np.pi/N))
v_new = np.zeros((N+1),dtype=np.float64)
v_old = np.zeros((N+1),dtype=np.float64)
num_iters = 100
v_old = v0
error = []
for i in range(num_iters):
v_new[1:N] = 1./3 * v_old[1:N] + 1./3 * (v_old[2:N+1] + v_old[0:N-1])
error.append(np.linalg.norm((v_new[1:N] - v_old[1:N]),np.inf) )
v_old[:] = v_new[:]
plt.plot(error/error[0])
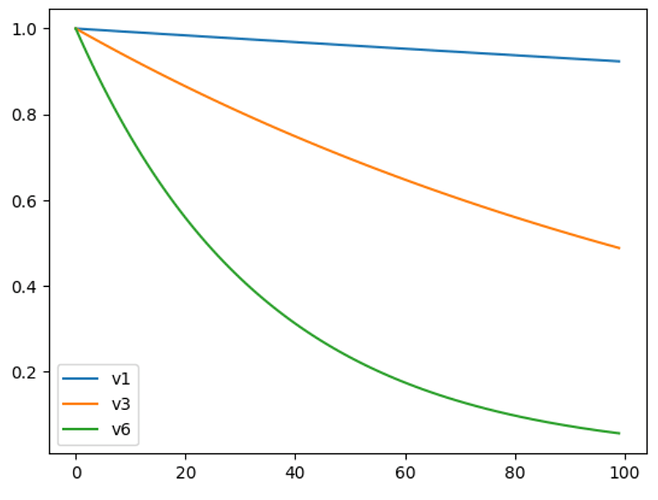
# 然后我们分别绘制v1,v3,v6的误差下降曲线
# 迭代公式完全一样,只有初始值不一样
def weighted_jacobian(v0, label):
v_new = np.zeros((N+1),dtype=np.float64)
v_old = np.zeros((N+1),dtype=np.float64)
num_iters = 100
v_old = v0
error = []
for i in range(num_iters):
v_new[1:N] = 1./3 * v_old[1:N] + 1./3 * (v_old[2:N+1] + v_old[0:N-1])
error.append(np.linalg.norm((v_new[1:N] - v_old[1:N]),np.inf) )
v_old[:] = v_new[:]
plt.plot(error/error[0], label=label)
# v1
v01 = np.zeros((N+1),dtype=np.float64)
for j in range(1,N):
v01[j] = 1/3 * (np.sin(j*np.pi/N))
weighted_jacobian(v01,'v1')
# v3
v03 = np.zeros((N+1),dtype=np.float64)
for j in range(1,N):
v03[j] = 1/3 * (np.sin(3*j*np.pi/N))
weighted_jacobian(v03,'v3')
# v6
v06 = np.zeros((N+1),dtype=np.float64)
for j in range(1,N):
v06[j] = 1/3 * (np.sin(6*j*np.pi/N))
weighted_jacobian(v06,'v6')
plt.legend()
可见,v1的收敛速度最慢,v3的收敛速度次之,v6的收敛速度最快。
所以,频率越高,收敛速度越快。
完毕。