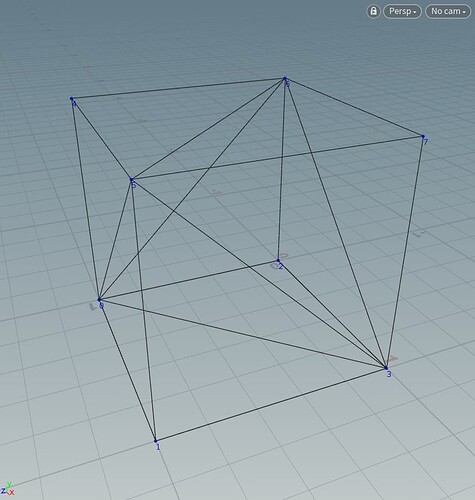
常常有这样一个需求:比如你有个体素网格,这些网格都是规整的立方体。但是你想要把立方体切割成四面体。这种在marching tetra等算法中是常见的。
问题归结为:怎么将立方体分割为四面体呢?
分割的方案是不唯一的,这里只给出一种简单的。
参考 Marching tetrahedra - Wikipedia
正中间放一个四面体,然后四面体的四个面各对应一个四面体。
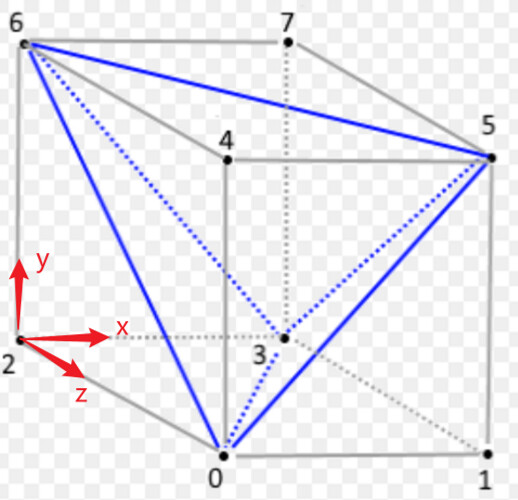
5个四面体的顶点编号为
0-3-5-6
0-1-3-5
0-2-3-6
0-4-5-6
3-5-6-7
顶点位置(假设边长为1)
0: (0,0,1)
1: (1,0,1)
2: (0,0,0)
3: (1,0,0)
4: (0,1,1)
5: (1,1,1)
6: (0,0,1)
7: (1,1,0)
为了保证四面体的四个面法线朝外,按照右手法则,四面体的四个三角面为(非必要,如果你只需要四面体而不需要三角面的话就不用)
0-3-5-6: 0-5-6, 0-3-5, 0-6-3, 3-6-5
0-1-3-5: 0-3-1, 0-5-3, 0-1-5, 1-3-5
0-2-3-6: 0-2-3, 0-3-6, 0-6-2, 2-6-3
0-4-5-6: 0-5-4, 0-4-6, 0-6-5, 4-5-6
3-5-6-7: 3-6-5, 3-7-5, 3-6-7, 5-6-7
代码:
import numpy as np
import meshio
def divide_cube_to_5_tetra(filename):
points = np.array([[0, 0, 1],
[1, 0, 1],
[0, 0, 0],
[1, 0, 0],
[0, 1, 1],
[1, 1, 1],
[0, 1, 0],
[1, 1, 0],
], dtype=np.float32)
tet_indices = np.array([ [0, 3, 5, 6],
[0, 1, 3, 5],
[0, 2, 3, 6],
[0, 4, 5, 6],
[3, 5, 6, 7]])
tri_indices = np.array([[0, 5, 6],
[0, 3, 5],
[0, 6, 3],
[3, 6, 5],
[0, 3, 1],
[0, 5, 3],
[0, 1, 5],
[1, 3, 5],
[0, 2, 3],
[0, 3, 6],
[0, 6, 2],
[2, 6, 3],
[0, 5, 4],
[0, 4, 6],
[0, 6, 5],
[4, 5, 6],
[3, 6, 5],
[3, 7, 5],
[3, 6, 7],
[5, 7, 6]])
cells = [
("tetra", tet_indices),
("triangle", tri_indices),
]
mesh = meshio.Mesh(
points,
cells,
)
meshio.tetgen.write(mesh, filename)
mesh.write(filename)
return mesh
if __name__ == "__main__":
divide_cube_to_5_tetra("cube_5_tetra.ply")
divide_cube_to_5_tetra("cube_5_tetra.vtk")
divide_cube_to_5_tetra("cube_5_tetra.node")
为了方便展示,分别写出了ply(houdini打开, 不是四面体), tetgen(tetview打开)和vtk(paraview打开)
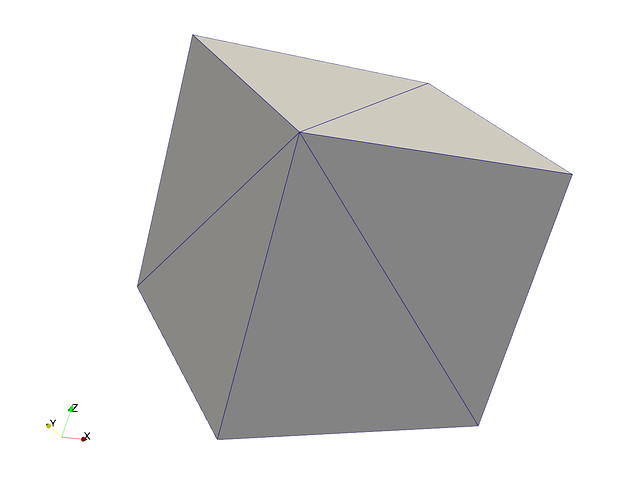
结果展示
(完毕,如有错误请指出)