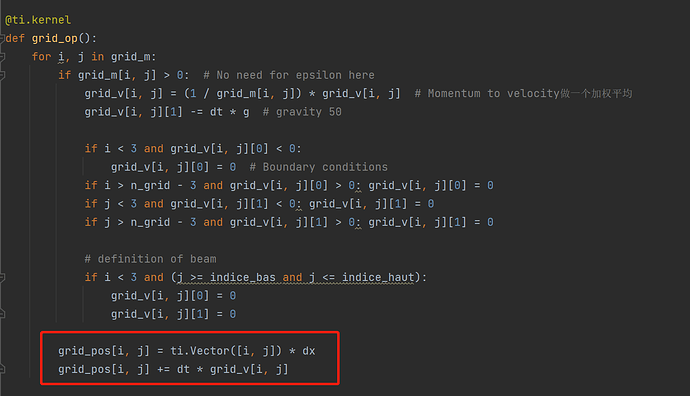
这是基于MPM128.py这个例子实现的悬臂弯曲,我想可视化模拟中中间网格的变化情况,但是我写出的网格位置是固定的,我想知道能否可视化这种变化状态吗,应该如何实现?
以下是相关代码:
import numpy as np
import taichi as ti
ti.init(arch=ti.cpu) # Try to run on GPU
quality = 1 # Use a larger value for higher-res simulations
n_particles, n_grid = 10000 * quality ** 2, 128 * quality
dx, inv_dx = 1 / n_grid, float(n_grid)
dt = 0.5e-4 / quality # 1e-4
elapsed_time = ti.field(dtype=float, shape=())
n_substeps = ti.field(dtype=int, shape=())
indice_temoin = ti.field(dtype=int, shape=())
p_vol, p_rho = (dx * 0.5) ** 2, 1
p_mass = p_vol * p_rho
E, nu = 500, 0.35 # Young's modulus and Poisson's ratio 0.1e5, 0.2
mu_0, lambda_0 = E / (2 * (1 + nu)), E * nu / (
(1 + nu) * (1 - 2 * nu)) # Lame parameters
x = ti.Vector.field(2, dtype=float, shape=n_particles) # position
v = ti.Vector.field(2, dtype=float, shape=n_particles) # velocity
C = ti.Matrix.field(2, 2, dtype=float,
shape=n_particles) # affine velocity field
F = ti.Matrix.field(2, 2, dtype=float,
shape=n_particles) # deformation gradient
material = ti.field(dtype=int, shape=n_particles) # material id
Jp = ti.field(dtype=float, shape=n_particles) # plastic deformation
grid_v = ti.Vector.field(2, dtype=float,
shape=(n_grid, n_grid)) # grid node momentum/velocity
grid_m = ti.field(dtype=float, shape=(n_grid, n_grid)) # grid node mass
grid_pos = ti.Vector.field(2, dtype=float, shape=(n_grid + 1, n_grid + 1))
# geometrical dimensions of beam
length_beam = 0.6
width_beam = 0.10
point_bas = 0.8 # 底部高度位置
# 以网格数为单位的梁底部和顶部高度位置的索引
indice_bas = int(point_bas * n_grid)
indice_haut = int(indice_bas + width_beam * n_grid)
gamma = 0.9999 # damping coefficient阻尼係數
g = 15
@ti.kernel
def p2g():
for i, j in grid_m:
grid_v[i, j] = [0, 0]
grid_m[i, j] = 0
for p in x: # Particle state update and scatter to grid (P2G)
base = (x[p] * inv_dx - 0.5).cast(int)
fx = x[p] * inv_dx - base.cast(float)
# Quadratic kernels [http://mpm.graphics Eqn. 123, with x=fx, fx-1,fx-2]
w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1) ** 2, 0.5 * (fx - 0.5) ** 2]
F[p] = (ti.Matrix.identity(float, 2) +
dt * C[p]) @ F[p] # deformation gradient update
h = ti.exp(10 * (1.0 - Jp[p])) # Hardening coefficient: snow gets harder when compressed
if material[p] == 1: # jelly, make it softer
h = 0.3
h = 1.0 # no change
mu, la = mu_0 * h, lambda_0 * h
if material[p] == 0: # liquid
mu = 0.0
U, sig, V = ti.svd(F[p])
J = 1.0
for d in ti.static(range(2)):
new_sig = sig[d, d]
if material[p] == 2: # Snow
new_sig = min(max(sig[d, d], 1 - 2.5e-2),
1 + 4.5e-3) # Plasticity
Jp[p] *= sig[d, d] / new_sig
sig[d, d] = new_sig
J *= new_sig
if material[p] == 0: # Reset deformation gradient to avoid numerical instability
F[p] = ti.Matrix.identity(float, 2) * ti.sqrt(J)
elif material[p] == 2:
F[p] = U @ sig @ V.transpose(
) # Reconstruct elastic deformation gradient after plasticity
stress = 2 * mu * (F[p] - U @ V.transpose()) @ F[p].transpose(
) + ti.Matrix.identity(float, 2) * la * J * (J - 1)
stress = (-dt * p_vol * 4 * inv_dx * inv_dx) * stress
affine = stress + p_mass * C[p]
for i, j in ti.static(ti.ndrange(
3, 3)): # Loop over 3x3 grid node neighborhood
offset = ti.Vector([i, j])
dpos = (offset.cast(float) - fx) * dx
weight = w[i][0] * w[j][1]
grid_v[base + offset] += weight * (p_mass * v[p] + affine @ dpos)
grid_m[base + offset] += weight * p_mass
@ti.kernel
def grid_op():
for i, j in grid_m:
if grid_m[i, j] > 0: # No need for epsilon here
grid_v[i, j] = (1 / grid_m[i, j]) * grid_v[i, j] # Momentum to velocity做一个加权平均
grid_v[i, j][1] -= dt * g # gravity 50
if i < 3 and grid_v[i, j][0] < 0:
grid_v[i, j][0] = 0 # Boundary conditions
if i > n_grid - 3 and grid_v[i, j][0] > 0: grid_v[i, j][0] = 0
if j < 3 and grid_v[i, j][1] < 0: grid_v[i, j][1] = 0
if j > n_grid - 3 and grid_v[i, j][1] > 0: grid_v[i, j][1] = 0
# definition of beam
if i < 3 and (j >= indice_bas and j <= indice_haut):
grid_v[i, j][0] = 0
grid_v[i, j][1] = 0
grid_pos[i, j] = ti.Vector([i, j]) * dx
grid_pos[i, j] += dt * grid_v[i, j]
@ti.kernel
def g2p():
for p in x: # grid to particle (G2P)
base = (x[p] * inv_dx - 0.5).cast(int)
fx = x[p] * inv_dx - base.cast(float)
w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1.0) ** 2, 0.5 * (fx - 0.5) ** 2]
new_v = ti.Vector.zero(float, 2)
new_C = ti.Matrix.zero(float, 2, 2)
for i, j in ti.static(ti.ndrange(
3, 3)): # loop over 3x3 grid node neighborhood
dpos = ti.Vector([i, j]).cast(float) - fx
g_v = grid_v[base + ti.Vector([i, j])]
weight = w[i][0] * w[j][1]
new_v += weight * g_v * gamma
new_C += 4 * inv_dx * weight * g_v.outer_product(dpos)
v[p], C[p] = new_v, new_C
x[p] += dt * v[p] # advection
old_elapsed_time = elapsed_time[None]
elapsed_time[None] += dt
n_substeps[None] += 1
if int(elapsed_time[None] / 0.1) > int(old_elapsed_time / 0.1):
print('elapsed time = ', elapsed_time[None])
@ti.kernel
def initialize():
for i in range(n_particles):
x[i] = [ti.random() * length_beam, ti.random() * width_beam + point_bas]
if x[i][0] > 0.98 * length_beam and indice_temoin[
None] == 0: # for printing evolution of one particle close to the end of beam
indice_temoin[None] = i
material[i] = 1 # 0: fluid 1: jelly 2: snow
v[i] = ti.Matrix([0, 0])
F[i] = ti.Matrix([[1, 0], [0, 1]])
Jp[i] = 1
elapsed_time[None] = 0.0
n_substeps[None] = 0
initialize()
print(
"info: oscillations will be small enough after elapsed time > 0.5; you can stop before by typing escape on beam "
"image")
gui = ti.GUI("Taichi MLS-MPM-99", res=1024, background_color=0x112F41)
limit_range = 30 # int(max(30,2e-3 // dt))
while (not gui.get_event(ti.GUI.ESCAPE, ti.GUI.EXIT)) and (elapsed_time[None] < 0.6):
for s in range(limit_range): # range(int(2e-3 // dt))
p2g()
grid_op()
g2p()
# print(x.to_numpy())
if n_substeps[None] % 400 == 0:
print("nb_steps = ", n_substeps[None], ", particule_temoin X = ", x[indice_temoin[None]][0],
", particule_temoin Y = ", x[indice_temoin[None]][1])
gui.circles(x.to_numpy(), radius=1.5, color=0x068587)
grid_pos_array = np.array(grid_pos.to_numpy())
print(grid_pos_array)
grid_pos_reshape = grid_pos_array.reshape((-1, 2, 1))
gui.circles(grid_pos_reshape, radius=1.5,color=0xF2B134)
# print(grid_pos.to_numpy())
gui.show()