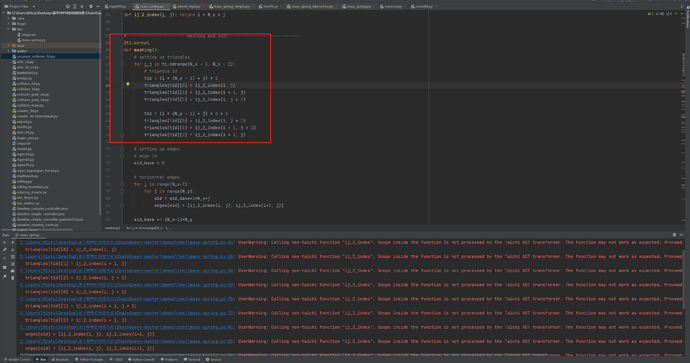
在运行09弹性体仿真的悬臂梁demo中,报错如下问题:
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:71: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
triangles[tid][2] = ij_2_index(i + 1, j)
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:81: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i, j), ij_2_index(i+1, j)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:81: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i, j), ij_2_index(i+1, j)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:88: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i, j), ij_2_index(i, j+1)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:88: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i, j), ij_2_index(i, j+1)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:95: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i+1, j), ij_2_index(i, j+1)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:95: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
edges[eid] = [ij_2_index(i+1, j), ij_2_index(i, j+1)]
C:\Users\Misty\Desktop\基于MPM的物理仿真\ChainQueen-master\demos\test\mass-spring.py:103: UserWarning: Calling non-taichi function “ij_2_index”. Scope inside the function is not processed by the Taichi AST transformer. The function may not work as expected. Proceed with caution! Maybe you can consider turning it into a @ti.func?
index = ij_2_index(i, j)
请问该如何解决?
原代码:
import taichi as ti
import math
ti.init(arch=ti.cpu)
# global control
paused = True
damping_toggle = ti.field(ti.i32, ())
curser = ti.Vector.field(2, ti.f32, ())
picking = ti.field(ti.i32,())
using_auto_diff = False
# procedurally setting up the cantilever
init_x, init_y = 0.1, 0.6
N_x = 20
N_y = 4
# N_x = 2
# N_y = 2
N = N_x*N_y
N_edges = (N_x-1)*N_y + N_x*(N_y - 1) + (N_x-1) * \
(N_y-1) # horizontal + vertical + diagonal springs
N_triangles = 2 * (N_x-1) * (N_y-1)
dx = 1/32
curser_radius = dx/2
# physical quantities
m = 1
g = 9.8
YoungsModulus = ti.field(ti.f32, ())
PoissonsRatio = ti.field(ti.f32, ())
LameMu = ti.field(ti.f32, ())
LameLa = ti.field(ti.f32, ())
# time-step size (for simulation, 16.7ms)
h = 16.7e-3
# substepping
substepping = 100
# time-step size (for time integration)
dh = h/substepping
# simulation components
x = ti.Vector.field(2, ti.f32, N, needs_grad=True)
v = ti.Vector.field(2, ti.f32, N)
total_energy = ti.field(ti.f32, (), needs_grad=True)
grad = ti.Vector.field(2, ti.f32, N)
elements_Dm_inv = ti.Matrix.field(2, 2, ti.f32, N_triangles)
elements_V0 = ti.field(ti.f32, N_triangles)
# geometric components
triangles = ti.Vector.field(3, ti.i32, N_triangles)
edges = ti.Vector.field(2, ti.i32, N_edges)
def ij_2_index(i, j): return i * N_y + j
# -----------------------meshing and init----------------------------
@ti.kernel
def meshing():
# setting up triangles
for i,j in ti.ndrange(N_x - 1, N_y - 1):
# triangle id
tid = (i * (N_y - 1) + j) * 2
triangles[tid][0] = ij_2_index(i, j)
triangles[tid][1] = ij_2_index(i + 1, j)
triangles[tid][2] = ij_2_index(i, j + 1)
tid = (i * (N_y - 1) + j) * 2 + 1
triangles[tid][0] = ij_2_index(i, j + 1)
triangles[tid][1] = ij_2_index(i + 1, j + 1)
triangles[tid][2] = ij_2_index(i + 1, j)
# setting up edges
# edge id
eid_base = 0
# horizontal edges
for i in range(N_x-1):
for j in range(N_y):
eid = eid_base+i*N_y+j
edges[eid] = [ij_2_index(i, j), ij_2_index(i+1, j)]
eid_base += (N_x-1)*N_y
# vertical edges
for i in range(N_x):
for j in range(N_y-1):
eid = eid_base+i*(N_y-1)+j
edges[eid] = [ij_2_index(i, j), ij_2_index(i, j+1)]
eid_base += N_x*(N_y-1)
# diagonal edges
for i in range(N_x-1):
for j in range(N_y-1):
eid = eid_base+i*(N_y-1)+j
edges[eid] = [ij_2_index(i+1, j), ij_2_index(i, j+1)]
@ti.kernel
def initialize():
YoungsModulus[None] = 1e6
paused = True
# init position and velocity
for i, j in ti.ndrange(N_x, N_y):
index = ij_2_index(i, j)
x[index] = ti.Vector([init_x + i * dx, init_y + j * dx])
v[index] = ti.Vector([0.0, 0.0])
@ti.func
def compute_D(i):
a = triangles[i][0]
b = triangles[i][1]
c = triangles[i][2]
return ti.Matrix.cols([x[b] - x[a], x[c] - x[a]])
@ti.kernel
def initialize_elements():
for i in range(N_triangles):
Dm = compute_D(i)
elements_Dm_inv[i] = Dm.inverse()
elements_V0[i] = ti.abs(Dm.determinant())/2
# ----------------------core-----------------------------
@ti.func
def compute_R_2D(F):
R, S = ti.polar_decompose(F, ti.f32)
return R
@ti.kernel
def compute_gradient():
# clear gradient
for i in grad:
grad[i] = ti.Vector([0, 0])
# gradient of elastic potential
for i in range(N_triangles):
Ds = compute_D(i)
F = Ds@elements_Dm_inv[i]
# co-rotated linear elasticity
R = compute_R_2D(F)
Eye = ti.Matrix.cols([[1.0, 0.0], [0.0, 1.0]])
# first Piola-Kirchhoff tensor
P = 2*LameMu[None]*(F-R) + LameLa[None]*((R.transpose())@F-Eye).trace()*R
#assemble to gradient
H = elements_V0[i] * P @ (elements_Dm_inv[i].transpose())
a,b,c = triangles[i][0],triangles[i][1],triangles[i][2]
gb = ti.Vector([H[0,0], H[1, 0]])
gc = ti.Vector([H[0,1], H[1, 1]])
ga = -gb-gc
grad[a] += ga
grad[b] += gb
grad[c] += gc
@ti.kernel
def compute_total_energy():
for i in range(N_triangles):
Ds = compute_D(i)
F = Ds @ elements_Dm_inv[i]
# co-rotated linear elasticity
R = compute_R_2D(F)
Eye = ti.Matrix.cols([[1.0, 0.0], [0.0, 1.0]])
element_energy_density = LameMu[None]*((F-R)@(F-R).transpose()).trace() + 0.5*LameLa[None]*(R.transpose()@F-Eye).trace()**2
total_energy[None] += element_energy_density * elements_V0[i]
@ti.kernel
def update():
# perform time integration
for i in range(N):
# symplectic integration
# elastic force + gravitation force, divding mass to get the acceleration
if using_auto_diff:
acc = -x.grad[i]/m - ti.Vector([0.0, g])
v[i] += dh*acc
else:
acc = -grad[i]/m - ti.Vector([0.0, g])
v[i] += dh*acc
x[i] += dh*v[i]
# explicit damping (ether drag)
for i in v:
if damping_toggle[None]:
v[i] *= ti.exp(-dh*5)
# enforce boundary condition
for i in range(N):
if picking[None]:
r = x[i]-curser[None]
if r.norm() < curser_radius:
x[i] = curser[None]
v[i] = ti.Vector([0.0, 0.0])
pass
for j in range(N_y):
ind = ij_2_index(0, j)
v[ind] = ti.Vector([0, 0])
x[ind] = ti.Vector([init_x, init_y + j * dx]) # rest pose attached to the wall
for i in range(N):
if x[i][0] < init_x:
x[i][0] = init_x
v[i][0] = 0
@ti.kernel
def updateLameCoeff():
E = YoungsModulus[None]
nu = PoissonsRatio[None]
LameLa[None] = E*nu / ((1+nu)*(1-2*nu))
LameMu[None] = E / (2*(1+nu))
# init once and for all
meshing()
initialize()
initialize_elements()
updateLameCoeff()
gui = ti.GUI('Linear FEM', (800, 800))
while gui.running:
picking[None]=0
# key events
for e in gui.get_events(ti.GUI.PRESS):
if e.key in [ti.GUI.ESCAPE, ti.GUI.EXIT]:
exit()
elif e.key == 'r':
initialize()
elif e.key == '0':
YoungsModulus[None] *= 1.1
elif e.key == '9':
YoungsModulus[None] /= 1.1
if YoungsModulus[None] <= 0:
YoungsModulus[None] = 0
elif e.key == '8':
PoissonsRatio[None] = PoissonsRatio[None]*0.9+0.05 # slowly converge to 0.5
if PoissonsRatio[None] >= 0.499:
PoissonsRatio[None] = 0.499
elif e.key == '7':
PoissonsRatio[None] = PoissonsRatio[None]*1.1-0.05
if PoissonsRatio[None] <= 0:
PoissonsRatio[None] = 0
elif e.key == ti.GUI.SPACE:
paused = not paused
elif e.key =='d' or e.key == 'D':
damping_toggle[None] = not damping_toggle[None]
elif e.key =='p' or e.key == 'P': # step-forward
for i in range(substepping):
if using_auto_diff:
total_energy[None]=0
with ti.Tape(total_energy):
compute_total_energy()
else:
compute_gradient()
update()
updateLameCoeff()
if gui.is_pressed(ti.GUI.LMB):
curser[None] = gui.get_cursor_pos()
picking[None] = 1
# numerical time integration
if not paused:
for i in range(substepping):
if using_auto_diff:
total_energy[None]=0
with ti.Tape(total_energy):
compute_total_energy()
else:
compute_gradient()
update()
# render
pos = x.to_numpy()
for i in range(N_edges):
a, b = edges[i][0], edges[i][1]
gui.line((pos[a][0], pos[a][1]),
(pos[b][0], pos[b][1]),
radius=1,
color=0xFFFF00)
gui.line((init_x, 0.0), (init_x, 1.0), color=0xFFFFFF, radius=4)
if picking[None]:
gui.circle((curser[None][0], curser[None][1]), radius=curser_radius*800, color=0xFF8888)
# text
gui.text(
content=f'9/0: (-/+) Young\'s Modulus {YoungsModulus[None]:.1f}', pos=(0.6, 0.9), color=0xFFFFFF)
gui.text(
content=f'7/8: (-/+) Poisson\'s Ratio {PoissonsRatio[None]:.3f}', pos=(0.6, 0.875), color=0xFFFFFF)
if damping_toggle[None]:
gui.text(
content='D: Damping On', pos=(0.6, 0.85), color=0xFFFFFF)
else:
gui.text(
content='D: Damping Off', pos=(0.6, 0.85), color=0xFFFFFF)
gui.show()