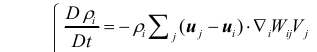我正在学习 SPH ,其理论公式是:
同时,我想跟着课程做一下作业:

我想先写一份python代码,然后再转成taichi代码。我的python代码是:
density = [0 for _ in range(len(ps.pos))]
v = 4/3*np.pi*(ps.support_radius**3)
for idx, p in enumerate(ps.pos):
for nbIdx in ps.particle_neighbors[idx]:
pos = ps.pos[nbIdx]
dis = np.linalg.norm(np.array(p) - np.array(pos))
density[idx] += v*ps.density[idx]*self.kernel(dis, ps.support_radius)
在这里,ps.density是初始密度,density是计算后的密度。
def kernel(self, dis, h):
if self.dim == 2:
k = 40 / 7 / np.pi
else:
k = 8 / np.pi
q = dis/h
res = 0
if q <= 1.0:
if q <= 0.5:
q2 = q * q
q3 = q2 * q
res = k * (6.0 * q3 - 6.0 * q2 + 1)
else:
res = k * 2 *((1 - q)**3)
return res
在初始阶段,也就是粒子还没开始散开的阶段:

在上面的代码中:ps.density=1000,但是计算后,np.max(density)=475.2
我运行github上的SPH代码,计算后的density也都是在1000左右。SPH的compute_densities跟视频过程不太一样。
求助:我自己的python代码,哪里有问题么?
我的可运行代码为:
import os.path
import numpy as np
class ParticleSystem:
# 用于记录粒子
def __init__(self):
self.dims = 2
self.particle_radius = 0.05 # 粒子半径
self.pos = [] # 记录粒子位置
self.bounds = [] # minx, maxx, miny, maxy, minz, maxz
'''
记录粒子所在位置的压力,这个压力并不是被粒子带着走的
当粒子位置变化了之后,压力是需要更新的
'''
self.pressure = []
self.density = []
self.velocity = []
'''
support radius的意思是说,在这个半径内,其他粒子对该粒子有影响
在这个半径外,其他粒子对该粒子无影响
'''
self.support_radius = self.particle_radius*4
'''
记录当前粒子的邻居,所谓邻居,就是与当前粒子的距离小于support radius的粒子
在计算密度,速度的微分等过程中,都需要计算邻居
'''
self.particle_neighbors = []
self.offset2 = [[x, y] for x in range(-1, 2) for y in range(-1, 2)]
self.offset3 = [[x, y, z] for x in range(-1, 2) for y in range(-1, 2) for z in range(-1, 2)]
def IsOutside(self, pos: list):
# 判断某个粒子是否在边界条件外
pass
def search_neighbors(self):
'''
计算邻居,本来应该是每两个点求距离,然后判断是否小于support_radius
但是,点太多了的话,求距离非常花时间
这里采用的方法,是先将区域画网格,然后在网格内的点才计算距离,减少计算
'''
gridNum = {}
for idx, p in enumerate(self.pos):
sub = self.pos_to_grid_sub(p)
index = self.sub_to_index(sub)
if index not in gridNum.keys():
gridNum[index] = []
gridNum[index].append(idx)
self.particle_neighbors = [[] for i in range(len(self.pos))]
for idx, p in enumerate(self.pos):
sub = self.pos_to_grid_sub(p)
if self.dims == 2:
offset = self.offset2
elif self.dims == 3:
offset = self.offset3
for of in offset:
newsub = [sub[0]+of[0], sub[1]+of[1]]
index = self.sub_to_index(newsub)
if index in gridNum.keys():
for ne in gridNum[index]:
distance = np.linalg.norm( np.array(p) - np.array(self.pos[ne]) )
if distance < self.support_radius and ne != idx:
self.particle_neighbors[idx].append(ne)
def pos_to_grid_sub(self, pos):
if not(( len(pos)==3 and len(self.bounds)==6 ) or (len(pos)==2 and len(self.bounds)==4)):
raise RuntimeError('coordinate wrong')
if self.dims == 2:
xmin, xmax, ymin, ymax = self.bounds
elif self.dims == 3:
xmin, xmax, ymin, ymax, zmin, zmax = self.bounds
gridX = int((pos[0] - xmin) / self.support_radius)
gridY = int((pos[1] - ymin) / self.support_radius)
if self.dims == 3:
gridZ = int((pos[2]-zmin)/self.support_radius)
if self.dims == 2:
return gridX, gridY
elif self.dims == 3:
return gridX, gridY, gridZ
def sub_to_index(self, sub):
if self.dims == 3:
index = sub[2]*self.Xlen*self.Ylen + sub[1]*self.Xlen + sub[0]
elif self.dims == 2:
index = sub[1] * self.Xlen + sub[0]
return index
class WaterParticleSystem(ParticleSystem):
def __init__(self):
super().__init__()
self.viscosity = 0.05 # viscosity
self.density0 = 1000
for x in np.arange(6, 9, 0.05):
for y in np.arange(2, 7, 0.05):
self.pos.append([x, y])
self.pressure.append(0) # 初始压力为0
self.density.append(self.density0)
self.velocity.append(0) # 初始速度
self.bounds = [0, 10, 0, 10]
self.Xlen = int((self.bounds[1] - self.bounds[0])/self.support_radius)
self.Ylen = int((self.bounds[3] - self.bounds[2])/self.support_radius)
def IsOutside(self, pos: list):
'''
定义二维边界,[0-10] x [0-10]
'''
x, y = pos
if x >= 0 and x <= 10 and y >=0 and y<=10:
return True
return False
class SPHSolver:
def __init__(self):
self.g = -0.98 # gravity
self.dt = 2e-4
self.dim = 2
def step(self, ps):
ps1 = self.substep(ps)
ps2 = self.enforce_boundary(ps1)
return ps2
def substep(self, ps):
self.compute_density(ps)
def enforce_boundary(self, ps):
pass
def compute_density(self, ps):
density = [0 for _ in range(len(ps.pos))]
v = 4/3*np.pi*(ps.support_radius**3)
for idx, p in enumerate(ps.pos):
for nbIdx in ps.particle_neighbors[idx]:
pos = ps.pos[nbIdx]
dis = np.linalg.norm(np.array(p) - np.array(pos))
density[idx] += v*ps.density[idx]*self.kernel(dis, ps.support_radius)
print(np.max(density))
def compute_non_pressure_forces(self):
pass
def compute_pressure_forces(self):
pass
def kernel(self, dis, h):
if self.dim == 2:
k = 40 / 7 / np.pi
else:
k = 8 / np.pi
q = dis/h
res = 0
if q <= 1.0:
if q <= 0.5:
q2 = q * q
q3 = q2 * q
res = k * (6.0 * q3 - 6.0 * q2 + 1)
else:
res = k * 2 *((1 - q)**3)
return res
if __name__ == '__main__':
ps = WaterParticleSystem()
solver = SPHSolver()
ps.search_neighbors()
solver.compute_density(ps)