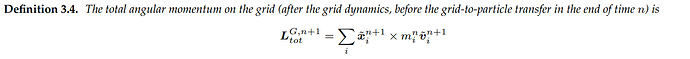大家好,最近看了胡老师的课,想学习一下蒋老师的‘‘The Affine Particle-In-Cell Method’’。阅读tech doc后,发现还是不太理解affine matrix是怎么推出来的,所以就想看看PIC的旋转动量到底是怎么减小的。自己尝试推导后,得出了旋转动量在P2G后守恒,G2P后减小的结论。但我在推导过程中有些步骤不太确定,大概用举例法验证了一下就往下写了。想请教一下大家,下面的推导正确吗?如果错误,麻烦推荐给我相关的资料,谢谢!
P2G前所有粒子的angular momentum是
\mathbf{L}_{tot}^{P,n} = \sum_p \mathbf{x}_p^n \times m_p \mathbf{v}_p^n
P2G后所有网格顶点的angular momentum是
\mathbf{L}_{tot}^{G,n} = \sum_i \mathbf{x}_i^n \times m_i^n \mathbf{v}_i^n
假设 \Delta t = 0, G2P前所有网格顶点的angular momentum是
\mathbf{L}_{tot}^{G,n+1} = \sum_i \mathbf{x}_i^n \times m_i^n \tilde{\mathbf{v}}_i^{n+1}
G2P后所有网格顶点的angular momentum是
\mathbf{L}_{tot}^{P,n+1} = \sum_p \mathbf{x}_p^n \times m_p \mathbf{v}_p^{n+1}
先进行P2G旋转动量守恒的推导,将 \mathbf{v}_i^n = \frac{\sum_{p} w_{ip}^n m_p\mathbf{v}_p^n}{m_i^n} 代入(2)式
\mathbf{L}_{tot}^{G,n} = \sum_i \mathbf{x}_i^n \times \sum_{p} w_{ip}^n m_p\mathbf{v}_p^n =- \sum_p m_p \mathbf{v}_p^n \times \sum_i w_{ip}^n \mathbf{x}_i^n
因为 \sum_i w_{ip}^n \mathbf{x}_i^n = \mathbf{x}_p^n ,上式变形为
\mathbf{L}_{tot}^{G,n} = - \sum_p m_p \mathbf{v}_p^n \times \mathbf{x}_p^n = \mathbf{L}_{tot}^{P,n}
因此P2G前后旋转动量守恒
然后进行G2P的推导,将 \mathbf{v}_p^{n+1} = \sum_i w_{ip}\mathbf{\tilde{v}}_i^{n+1} 代入 (4)式
\mathbf{L}_{tot}^{P,n+1} = \sum_p \mathbf{x}_p^n \times m_p \sum_i w_{ip}^n\mathbf{\tilde{v}}_i^{n+1}
因为 \sum_i w_{ip}^n \mathbf{x}_i^n = \mathbf{x}_p^n , 上式变形为
\mathbf{L}_{tot}^{P,n+1} = \sum_p \sum_i w_{ip}^n \mathbf{x}_i^n \times m_p \sum_i w_{ip}^n\mathbf{\tilde{v}}_i^{n+1} = \sum_p \sum_i (w_{ip}^n)^2 \mathbf{x}_i^n \times m_p \mathbf{\tilde{v}}_i^{n+1}
对比G2P前网格顶点的旋转动量,将 m_i^n = \sum_p w_{ip}^n m_p 代入 (3)式
\mathbf{L}_{tot}^{G,n+1} = \sum_i \mathbf{x}_i^n \times m_i^n \tilde{\mathbf{v}}_i^{n+1} = \sum_i \mathbf{x}_i^n \times \sum_p w_{ip}^n m_p \tilde{\mathbf{v}}_i^{n+1} = \sum_p \sum_i w_{ip}^n \mathbf{x}_i^n \times m_p \tilde{\mathbf{v}}_i^{n+1}
对比 (8)式,每一项都多乘了个 w_{ip}<1 的系数,所以G2P后粒子的总旋转动量变小了。
09.22 更新
今天再读文章,思路清晰一些了,原来每个粒子angular momentum的损失文章很清楚在(4)式写明了, 需要对上面的公式进行进一步变换。
根据 (7) 式,改变一下 \sum 操作符的顺序
\mathbf{L}_{tot}^{P,n+1} = \sum_p \mathbf{x}_p^n \times m_p \sum_i w_{ip}^n\mathbf{\tilde{v}}_i^{n+1} = \sum_p \sum_i \mathbf{x}_p^n \times m_p w_{ip}^n\mathbf{\tilde{v}}_i^{n+1}
再对(9)式改变一下 w_{ip} 的位置
\mathbf{L}_{tot}^{G,n+1} = \sum_p \sum_i w_{ip}^n \mathbf{x}_i^n \times m_p \tilde{\mathbf{v}}_i^{n+1} = \sum_p \sum_i \mathbf{x}_i^n \times m_p w_{ip}^n \tilde{\mathbf{v}}_i^{n+1}
上两式相减为G2P总共损失的旋转动量。那么对于每一个粒子,减少的旋转动量就是:
\mathbf{L}_p^{n+1} = \sum_i (\mathbf{x}_p^n-\mathbf{x}_i^n) \times m_p w_{ip}^n \tilde{\mathbf{v}}_i^{n+1}
除了 \mathbf{x}_i^n 在文章中记为 \mathbf{x}_i 以外, 上式子与文章中(4)式相同。
现在感觉能理解文章的思路了,我接着往下看了~
蒋老师2017年JCP的文章写得更深入了,之后有时间好好研究一下!我还是先把代码运行起来!