简介
Taichi 是一门开源的，嵌入在 Python 中的高性能并行计算语言。相较于一些传统的数值计算用语言（Fortran / C++），Taichi 提供了如下的优势：
-
简单易用：Taichi 的语法和 Python 极为类似，最大限度降低了并行程序学习和编写的门槛
-
数据结构：Taichi 提供了专门为数值计算设计的
ti.field，实现了计算代码和数据结构的解耦，用户可以在不修改计算逻辑的情况下灵活调试数据的行列主序
同时，相较于数值计算用户熟悉的 Matlab / Numpy 等工具，Taichi 则在性能上提供了大幅强化：
-
超高性能：Taichi 使用独自的 JIT 即时编译技术将用户代码编译成原生的 CPU 或 GPU 机器码，相较于解释型语言的性能提升可达数个量级
-
可移植性：Taichi 可运行于不同的后端（CPU，CUDA，Metal，OpenGL 等等）且无需用户修改原代码
Taichi 的这些特性使得其在数值计算算法实现中体现出其他语言不可比拟的优势，有越来越多的学者/研究小组将 Taichi 作为算法实现的工具语言：
不仅如此，由于 Taichi 易于安装，几乎不存在附加依赖，使得用户复现他人代码变得前所未有的轻松，因此我们相信 Taichi 将极大地促进数值计算用户间的学术科研交流。
安装
Taichi 作为一个 Python 包的形式出现，用户安装 Taichi 和安装 Python 包一样容易，完全省去了折腾软件依赖的麻烦。首先确认你已经有 pip 并更新到了最新版本：
pip3 install pip --upgrade
假设你的 Python 版本是 3.0 以上，你仅需要这一条指令来安装 Taichi：
pip3 install -U taichi
然后你就可以尝试运行 Taichi 程序了！我们提供了丰富的 example 示例代码
ti example
你可以在命令行中选择自己感兴趣的 example，输入编号即可运行。
我们近期也添加了更加便于交互的 gallery 功能，便于用户用 GUI 界面来浏览选择自己喜欢的示例
ti gallery
用 Taichi 编写数值计算代码的优势
Taichi 创始的初衷，就是解决数值计算用户在 编程效率 和 运行性能 间的冲突；为了让用户可以用更少的代码，写出更快更强性能的数值计算程序，Taichi 提供了如下的特性：
易用的高性能并行计算
传统的并行计算语言要求用户对于计算机硬件有比较多的了解，在代码编写过程中甚至需要手动申请，释放内存（CUDA），手动分配调度线程块（Numba / CUDA）等。在 Taichi 中，并行计算代码的编写几乎和串行代码一样直白容易，比如用有限差分计算一个 1 维变量的 1 阶和 2 阶导数在 Taichi 中可以这样书写：
f = ti.field(dtype=ti.f64, shape=(128,))
dfdx = ti.field(dtype=ti.f64, shape=(128,))
d2fdx = ti.field(dtype=ti.f64, shape=(128,))
dx = 1e-3
@ti.kernel
def diff():
for i in range(1,128):
dfdx[i] = (f[i] - f[i-1]) / dx
for i in range(1,127):
d2fdx[i] = (f[i-1] - 2*f[i] + f[i+1]) / dx**2
不仅如此，在 Taichi 中，用户只需要修改 Taichi 初始化时的一条指令，就可以让自己的程序运行在多核 CPU（如 x64， Arm）和 GPU（如 CUDA） 等多种后端上，完全无需顾虑底层硬件的变化：
ti.init(arch=ti.cpu) # Run on CPU backend
ti.init(arch=ti.cuda) # Run on CUDA backend
这一点在很多的现有工具中都是几乎不可能的。例如在 Python 高性能计算用户中比较流行的 Numba 中，需要用户针对 CPU 和 CUDA 后端编写不同的代码，其中 CUDA 后端的代码编写和 CUDA 的原生接口极为类似，对于数值计算用户来说学习负担较大，代码维护也很不方便。
关于 Taichi 和 Numba / CUDA 的易用性及性能 benchmark 对比，我们有发布一篇技术博客以及一个完整的仓库可供参考。
灵活的数据排布
在数值计算任务中，多维数组的内存排布对于计算性能是至关重要的，而 Taichi 中基础的数据容器 ti.field 是专门为数值计算用户设计的数据结构，其创建和访问很类似于一般语言中的多维数组，或者是 Numpy 中的 Ndarray：
f = ti.field(dtype=ti.f64, shape=(128,128)) # Creates a 2D 128x128 field
@ti.kernel
def init():
for i,j in f:
f[i,j] = 0.0. # Access field elements
在此基础之上，ti.field 将传统语言中非常头疼的数据排布问题彻底简化：
a = ti.field(dtype=ti.i32, shape=(n, m), order='ij') # explicit row major
b = ti.field(dtype=ti.i32, shape=(n, m), order='ji') # explicit column major
@ti.kernel
def access():
for i,j in a:
a[i,j] += 1.0
for i,j in b:
b[i,j] += 1.0
注意到 a 和 b 的访问形式是完全相同的，用户仅需要在声明时指定 order 即可实现不同排布。
相比之下，在传统的 C/C++ 类型语言中，你需要显式地调整数据的排布和访问顺序：
int a[3][2]; // row-major
int b[2][3]; // column-major
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 2; j++) {
do_something(a[i][j]);
do_something(b[j][i]);
}
}
这个调整的难度在 3 维甚至以上的维度时会变得极其繁复且难以检查。关于 Taichi 中的数据排布，可以参考官方文档。
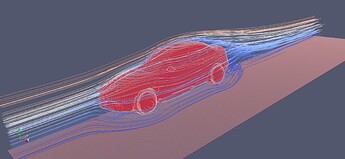
用 Taichi 编写的流体仿真示例
在 taichi-fluid 中收录了现在我们掌握的来自社区的 CFD 方向的项目，以下列举一些：
-
MAC（欧拉视角）
GitHub - takah29/2d-fluid-simulator: 2D incompressible fluid solver implemented in Taichi.
GitHub - houkensjtu/MAC-taichi: A MAC (Marker-And-Cell) solver written in Taichi
-
SPH（拉格朗日视角）
GitHub - erizmr/SPH_Taichi: A high-performance implementation of SPH in Taichi.
-
FLIP/APIC（混合欧拉拉格朗日）
GitHub - nepluno/pyasflip: Python implementation of the ASFLIP advection method
-
LBM（玻尔兹曼）
GitHub - hietwll/LBM_Taichi: Fluid solver based on Lattice Boltzmann method implemented by taichi programming language
GitHub - yjhp1016/taichi_LBM3D: A 3D sparse LBM solver implemented using Taichi
Benchmark
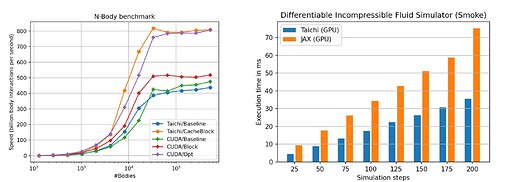
我们在 taichi_benchmark 中给出了大量 Taichi 与其他常见语言实现的性能对比数据，并且我们公开了完整的测试代码，可供用户在自己的硬件环境中测试。（我们的测试硬件平台一般为 i9-11900K / RTX 3080)
我们测试的项目包括了基本运算模式：比如规约求和 (reduce_sum)，矩阵元素相乘求和运算 (SAXPY)等：
同时也有实际的数值计算案例，比如 N-body 问题求解，MAC 法中的显式速度场更新，可微不可压缩流体仿真等：
在性能对比中 Taichi 往往可以用极其简洁的代码实现接近甚至小幅超越同等语义 CUDA 代码的计算性能，并在一些算例中大幅超过 Numpy / Numba 等工具的性能。
数值计算兴趣小组 （Numerical Computation SIG） 简介
为了促进数值计算用户的互相学习和交流，进一步降低用户解答疑惑时的负担与门槛，我们设立了 Taichi 数值计算 SIG （Special Interest Group），群组成员可以通过微信群组进行技术讨论，并在每周五组织高质量的数值计算线上分享活动，广泛讨论数值计算中大家关心的问题。目前为止的活动中我们的议题包括：
-
数值计算数学基础
-
流体数值计算基础（有限体积法 / SIMPLE 算法）
-
高性能并行计算基础
-
PBD 软体仿真 Taichi 实现实战
活动的录像在 B 站进行了公开：
了解更多
Taichi CFD 合集：GitHub - houkensjtu/taichi-fluid: A collection of CFD related resources for Taichi developers.
Taichi 语言官网：https://taichi-lang.cn/
Taichi 语言开源代码：GitHub - taichi-dev/taichi: Productive & portable high-performance programming in Python.
Taichi 数值计算 SIG 小组：关于数值计算兴趣小组，内含分享排期（板块必读~）
太极图形 b 站数值计算合集：如何用 Taichi 实现数值计算？（持续更新，可收藏后反复观看）_哔哩哔哩_bilibili