在有限元，弹性力学和塑性力学的课上经常会听到弹塑性力学。
而在图形学领域貌似很少听到有人谈论弹塑性，大多数用的词是“粘弹性”。
甚至还有些地方，我看到有说“粘-弹-塑性介质”的。
既然弹性体是表现弹性，而塑形体则表现为流动。粘性体同样表现流动。两者到底有什么区别呢？或者说，什么时候该用哪个术语呢？
我不是专家，但是我说一下我的理解哈。抛砖引玉。
弹性和塑性分别就是变形之后是否能够恢复原状，这个过程和时间无关。
而粘性的表现就是物体的形变，本构方程和时间也有关系。
1 个赞
感谢师兄的回复。这些天我旁听了一些塑性力学的课并且看了一些连续介质力学的书。我的总结如下：
1）该问题属于连续介质力学。
2）简单来说，确实是和时间有关系的。
一句话：弹塑性力学的关注点是变形的多少， 而粘性关注的是变形的快慢。
弹塑性力与粘性力两者都是抵抗剪切变形的。但弹塑性力的大小是
由剪切变形（切应变）的大小决定的。而粘性力是由剪切变形的速率的大小（切
应变率）决定的。也就是后者比前者多了一个时间的导数。我们可以想象如下一
个实验。
不那么严谨地，如果我们仿照牛顿平板粘性实验：
在不同的问题中，关注点不一样：
假如我们是想研究一个大桥的变形，因为该变形是如此缓慢，以至于变形的快慢无关紧要了，但是变形的多少非常关键，因为一点点小的变形可能就会造成危险。
假如我们想研究飞机或者火箭与空气的摩擦。因为速度是如此之快（空气是静止的，而飞机在高速移动），所以变形的快慢非常关键，粘性力的影响也会非常之大。
3） 那么，在公式上是如何体现的呢？
一句话：前者（弹塑性）关注的是应变（即表示变形的多少），而后者关注的是应变率（即变形的快慢）
细说：
弹性应力中的剪切分量由广义胡克定律给出：
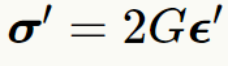
粘性力的本构由广义牛顿内摩擦定律给出：
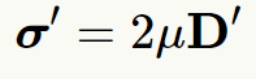
其中sigma’是应力偏量。mu是粘度。G是剪切模量。epsilon‘是应变偏量。D’是剪切应变率。
可见，两者的差别就在于剪切应变和剪切应变率！
4） 单位上的差别
我在之前的一个帖子里面问过一个问题： 固体拉梅参数mu和流体动力粘度mu是一回事吗？ - 中文讨论区 - Taichi
剪切模量的单位：N/m^2（或者说是Pa)
动力粘度的单位：Ns/m^2（或者说是Pa s)
从这里就能看出一些端倪：两者的单位就差一个时间！
2 个赞
补充：
5）粘性和弹性的组合：麦克斯韦模型！
在连续介质力学之中，可以共同处理这三种力学性质。
显然任何真实材料都是共同拥有弹性、塑性和粘性这三种性质的
关键在于问题关注哪一方面。
那么，有没有把这三者结合起来的模型呢？
有的！
有一个模型，叫麦克斯韦模型（没错就是那个大名鼎鼎的麦克斯韦），它就是把粘性和弹性结合了起来！
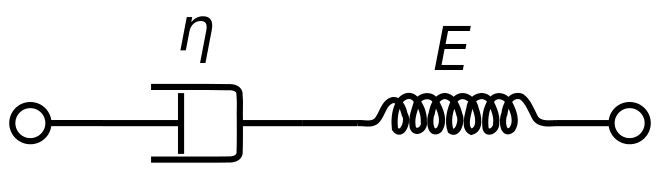
你看，滑块（或者叫粘壶）就代表粘性，弹簧就代表弹性。
写成公式就是这样的：
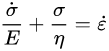
受麦克斯韦的启发，各路大神又发明了一大堆模型，基本就是组合来组合去
譬如开尔文-福格特模型（串联改成并联）
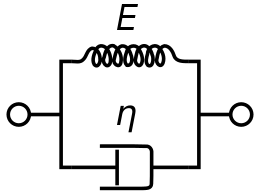
伯格斯模型（Burgers)
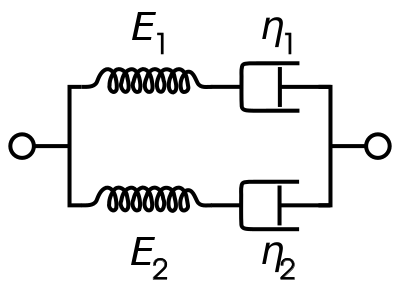
甚至可以弄得更复杂一点。
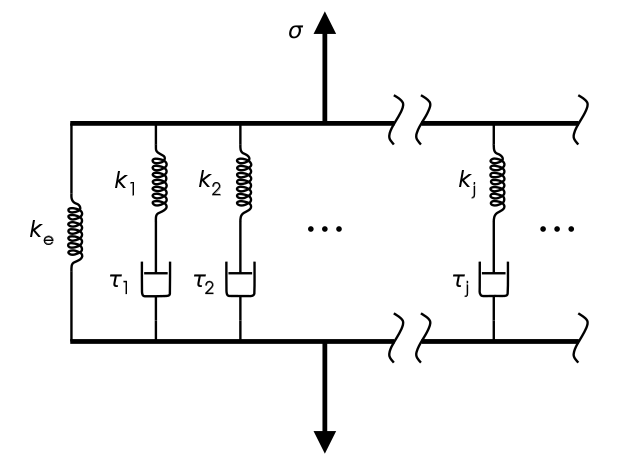
这样，粘弹性的问题就转化为了电路串并联的问题，即直观又简洁。
具体用什么，还是要看材料的哪种性质占主导
1 个赞