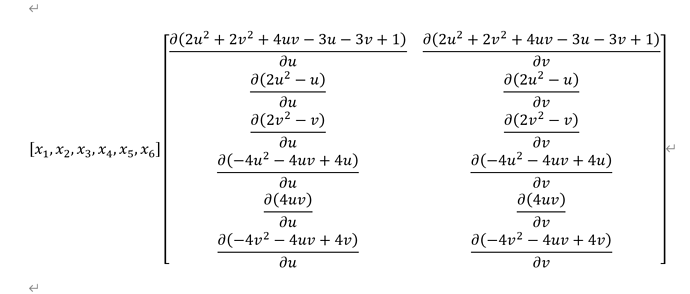我希望能够把线性有限元扩展为二阶或三阶FEM,我参考了2020 siggraph course Dynamic Deformables通过FEM直接构造deformation gradient方法。但是高阶basis function关于u,v求一阶导数得到的deformation gradient不是常数矩阵,请问这个时候该如何处理呢?比如下面的二阶FEM,论文中提到要选取quadrature point,我不太明白是什么意思?(我的理解是:比如可以选取三个高斯求积点,然后按照高斯权重加起来,不知道这种理解方式对不对?)
此外,我之前学过工程上FEM一般是写Galerkin方程,作用上test function后求积分再离散化,类似于GAMES201第六讲中线弹性方程的求解方法。课上学习的线性有限元和这种方式是等价的吗?如果想要把线性有限元写成Galerkin有限元方程应该是什么样的呢?
非常感谢!!