运行环境
[Taichi] version 0.8.6, llvm 10.0.0, commit d5f18ffd, osx, python 3.8.1
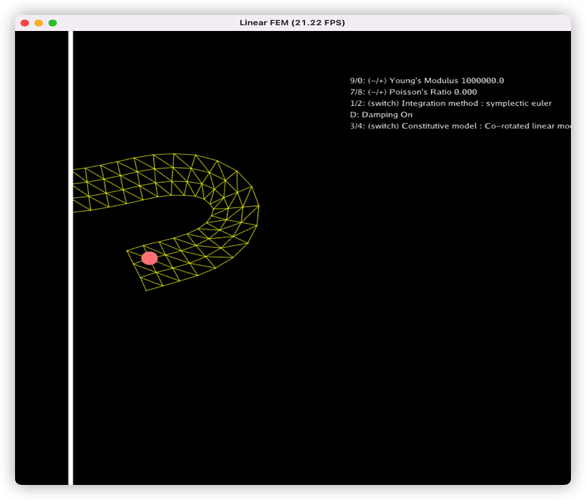
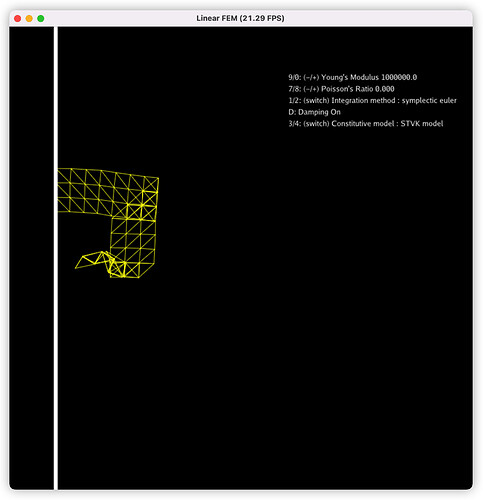
问题描述
我利用Explicit FEM方法实现弹簧。但STVK本构模型会出现弹簧自折叠的表现,Co-rotated则不会。请问是我的实现方式有问题,还是STVK模型本身的原因啊?
代码链接
[作业链接]https://github.com/yuhanZhou1/Taichi/blob/main/Explicit_FEM
核心代码:
# gradient of elastic potential
for i in range(N_triangles):
Ds = compute_D(i)
F = Ds@elements_Dm_inv[i]
# co-rotated linear elasticity
R = compute_R_2D(F)
Eye = ti.Matrix.cols([[1.0, 0.0], [0.0, 1.0]])
if model == 1:
# Strain stress
Estvk = 0.5 * (F.transpose() @ F - Eye)
# first Piola-Kirchhoff tensor
P = F @ (2 * LameMu[None] * Estvk + LameLa[None] * Estvk.trace() * Eye)
#assemble to gradient
H = elements_V0[i] * P @ (elements_Dm_inv[i].transpose())
a,b,c = triangles[i][0],triangles[i][1],triangles[i][2]
gb = ti.Vector([H[0,0], H[1, 0]])
gc = ti.Vector([H[0,1], H[1, 1]])
ga = -gb-gc
grad[a] += ga
grad[b] += gb
grad[c] += gc
elif model == 2:
# first Piola-Kirchhoff tensor- SameWay,diff write
# P = 2*LameMu[None]*(F-R) + LameLa[None]*((R.transpose())@F-Eye).trace()*R
# Strain stress
Co_rotated = (R.transpose())@F-Eye
# first Piola-Kirchhoff tensor
P = R @ (2 * LameMu[None] * Co_rotated + LameLa[None] * Co_rotated.trace() * Eye)
#assemble to gradient
H = elements_V0[i] * P @ (elements_Dm_inv[i].transpose())
a,b,c = triangles[i][0],triangles[i][1],triangles[i][2]
gb = ti.Vector([H[0,0], H[1, 0]])
gc = ti.Vector([H[0,1], H[1, 1]])
ga = -gb-gc
grad[a] += ga
grad[b] += gb
grad[c] += gc