在这里分享一个小问题的解决。
这个问题虽然不是很难,但是有点绕。新手可能会困惑,浪费一些时间。因此想到后面的同学们可能会有相同的困扰,在此总结如下:
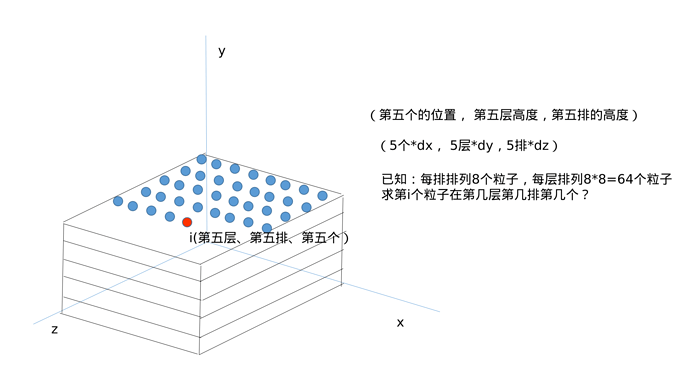
问题的产生:在初始排列的时候,如果采用随机初始化的做法,会导致粒子排列过于密集。在SPH中过密集的粒子会产生极大的斥力,导致一开始像爆炸一样的BUG。
解决方案就是一个个地整齐排列粒子。这不是很难,但是就像小学奥数题一样有点绕。
问题的解决:
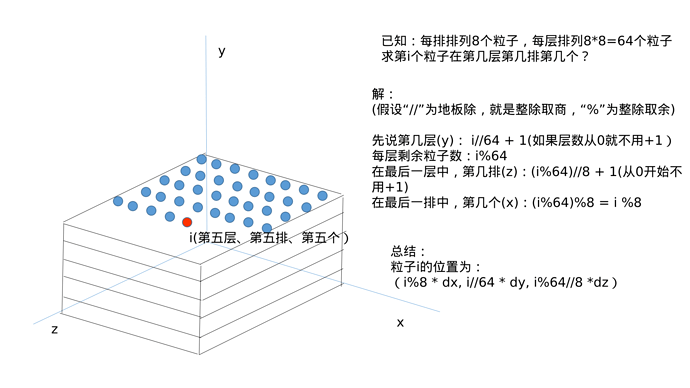
因此我们可以修改k-ye的PBF2d代码为3D情况的初始排列:
@ti.kernel
def init():
init_pos = ti.Vector([0.2,0.3,0.2])
cube_size = 0.4
spacing = 0.02
num_per_row = (int) (cube_size // spacing)
num_per_floor = num_per_row * num_per_row
for i in range(num_particles):
floor = i // (num_per_floor)
row = (i % num_per_floor) // num_per_row
col = (i % num_per_floor) % num_per_row
positions[i] = ti.Vector([row*spacing, floor*spacing, col*spacing]) + init_pos
完毕
1 个赞
说起这个,就想提一下之前Mingrui Zhang的SPH代码里生成一个粒子整齐排列的cube的程序很好,而且是二三维通用的。我提炼出来了主干:
import numpy as np
from functools import reduce # 整数:累加;字符串、列表、元组:拼接。lambda为使用匿名函数
def add_cube(lower_corner, cube_size, offset):
# lower_corner: corrdinate of left-down corner, exp. [1.0, 2.0, 3.0] or [1.0, 2.0]
# cube_size: length of each edge, exp. [10, 20, 30] or [10.0, 20.0]
# offset: offset distance, usually the diameter of particle, exp. 2.0
dim = len(lower_corner)
num_dim = []
range_offset = offset
for i in range(dim):
num_dim.append(np.arange(lower_corner[i] + 0.5 * offset, lower_corner[i] + cube_size[i] + 1e-5, range_offset))
num_new_particles = reduce(lambda x, y: x * y, [len(n) for n in num_dim])
new_positions = np.array(np.meshgrid(*num_dim, sparse=False, indexing='ij'), dtype=np.float32)
new_positions = new_positions.reshape(-1, reduce(lambda x, y: x * y, list(new_positions.shape[1:]))).transpose()
return num_new_particles, new_positions
if __name__ == "__main__":
print("hallo test adding a cube in whatever 2d or 3d!")
num_new_particles2, new_positions2 = add_cube([0.0, 0.0], [16.0, 24.0], 8.0)
num_new_particles3, new_positions3 = add_cube([0.0, 0.0, 0.0], [16.0, 24.0, 32.0], 8.0)
PS:后来查了一下发现,meshgrid里并非用’ijk’表示3D,大于2D的情况仍是使用’ij’。它的’ij’和’xy’只是区分矩阵索引和笛卡尔索引。
4 个赞