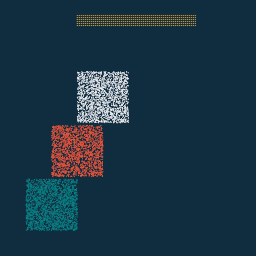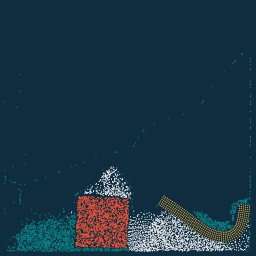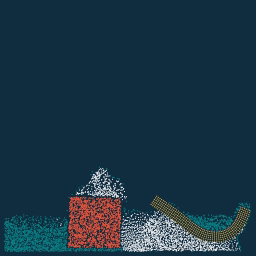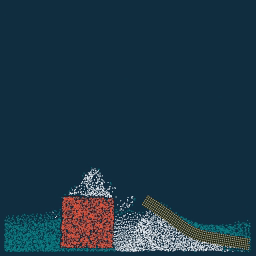其实就是把 mpm_99 复制粘贴到了 mpm_lagrangian_forces 里面,抄了一些导数的式子,免去了自动求导。
去掉自动求导之后似乎快了不少。
实验结果见 https://www.bilibili.com/video/BV1SV411z76R/
实现了三种边界情况,可以看到 sticky 的边界条件下水没法沿着边界向上滑动,靠近边界的物质看起来也不怎么容易移动。
separate 与 slip 边界条件很相像,但是因为 slip 边界条件不允许在边界上出现法向量方向的速度,水珠在 y 的上边界(或者说天花板)不会怎么受到重力作用,下落速度大大减慢,表现出在天花板上滑动。
References:
GAMES201
mpm_99, mpm_lagrangian_forces (from ti example)
Barbic and Sifakis’ SIGGRAPH Course notes on FEM / Model Reduction (2012)
Jiang et al. SIGGRAPH Course: The Material Point Method for Simulating Continuum Materials (2016)
import taichi as ti, sys
ti.init(debug = False, arch = ti.gpu)
bc_mode = int(sys.argv[1]) if len(sys.argv) > 1 else 2 # 0 for sticky; 1 for slip; 2 for separate
real = ti.f32
dim = 2
n_particle_x = 60
n_particle_y = 6
n_each = 2048
n_material = 3
n_mesh = n_particle_x * n_particle_y
n_particles = n_mesh + n_each * n_material
n_elements = (n_particle_x - 1) * (n_particle_y - 1) * 2
n_grid = 128
dx = 1 / n_grid
dx_inv = 1 / dx
dt = 2e-5
n_subframes = int(2e-3 // dt)
rho_p = 1
vol_p = (dx * 0.5) ** 2
m_p = vol_p * rho_p
E, nu = 5e3, 0.2
mu_0, lambda_0 = E / (2 * (1 + nu)), E * nu / ((1 + nu) * (1 - 2 * nu)) # Lame parameters
x_mesh_0, y_mesh_0 = 0.3, 0.9
dx_mesh = dx
bound = 3
x = ti.Vector.field(2, dtype = ti.f32, shape = n_particles)
v = ti.Vector.field(2, dtype = ti.f32, shape = n_particles)
f = ti.Vector.field(2, dtype = ti.f32, shape = n_particles)
C = ti.Matrix.field(2, 2, dtype = ti.f32, shape = n_particles)
Jp = ti.field(dtype = ti.f32, shape = n_particles)
material = ti.field(dtype = ti.i32, shape = n_particles)
vertices = ti.Vector.field(3, dtype = ti.i32, shape = n_elements)
B = ti.Matrix.field(2, 2, dtype = ti.f32, shape = n_elements)
WD = ti.Matrix.field(2, 2, dtype = ti.f32, shape = n_elements)
F = ti.Matrix.field(2, 2, dtype = ti.f32, shape = n_particles)
v_grid = ti.Vector.field(2, dtype = ti.f32, shape = (n_grid, n_grid))
m_grid = ti.field(dtype = ti.f32, shape = (n_grid, n_grid))
gravity = ti.Vector.field(2, dtype = ti.f32, shape = ())
@ti.func
def ij2p(i, j):
return i * ti.static(n_particle_y) + j
@ti.func
def get_T(vertices):
a = x[vertices[0]] - x[vertices[2]]
b = x[vertices[1]] - x[vertices[2]]
return ti.Matrix([[a.x, b.x], [a.y, b.y]])
@ti.kernel
def init():
gravity[None] = ti.Vector([0, -9.8 * 10])
for i, j in ti.ndrange(n_particle_x, n_particle_y):
p = ij2p(i, j)
x[p] = [x_mesh_0 + i * dx_mesh, y_mesh_0 + j * dx_mesh]
v[p] = ti.Vector.zero(ti.f32, 2)
C[p] = ti.Matrix.identity(ti.f32, 2)
material[p] = 3
for i, j in ti.ndrange(n_particle_x - 1, n_particle_y - 1):
e = i * (n_particle_y - 1) + j
vertices[e * 2] = ti.Vector([ij2p(i, j), ij2p(i + 1, j), ij2p(i, j + 1)])
tmp = get_T(vertices[e * 2])
B[e * 2] = tmp.inverse()
WD[e * 2] = -ti.abs(tmp.determinant()) / 2 * tmp.inverse().transpose()
vertices[e * 2 + 1] = ti.Vector([ij2p(i + 1, j + 1), ij2p(i, j + 1), ij2p(i + 1, j)])
tmp = get_T(vertices[e * 2 + 1])
B[e * 2 + 1] = tmp.inverse()
WD[e * 2 + 1] = -ti.abs(tmp.determinant()) / 2 * tmp.inverse().transpose()
for p in range(n_each * n_material):
x[p + n_mesh] = [ti.random() * 0.2 + 0.1 + 0.1 * (p // n_each), ti.random() * 0.2 + 0.1 + 0.21 * (p // n_each)]
v[p + n_mesh] = [0, 0]
F[p + n_mesh] = ti.Matrix.identity(ti.f32, 2)
Jp[p + n_mesh] = 1
C[p + n_mesh] = ti.Matrix.zero(ti.f32, 2, 2)
material[p + n_mesh] = p // n_each
@ti.kernel
def get_force():
for e in vertices:
F_tmp = get_T(vertices[e]) @ B[e]
J = F_tmp.determinant()
mu, la = mu_0 * 1e-3, lambda_0 * 1e-3
P = mu * (F_tmp - F_tmp.transpose().inverse()) + la * ti.log(J) * F_tmp.transpose().inverse()
H = P @ WD[e] * 1e-3 * (8 * n_grid ** 2) # TODO: magic number
tmp_x = ti.Vector([H[0, 0], H[1, 0]])
tmp_y = ti.Vector([H[0, 1], H[1, 1]])
f[vertices[e].x] += tmp_x
f[vertices[e].y] += tmp_y
f[vertices[e].z] += -tmp_x - tmp_y
@ti.kernel
def p2g():
for p in x:
base = (x[p] * dx_inv - 0.5).cast(int)
local = x[p] * dx_inv - base
w = [0.5 * (1.5 - local) ** 2, 0.75 - (local - 1) ** 2, 0.5 * (local - 0.5) ** 2]
affine = m_p * C[p]
if material[p] != 3:
F[p] = (ti.Matrix.identity(ti.f32, 2) + dt * C[p]) @ F[p]
U, sig, V = ti.svd(F[p])
if material[p] == 0:
J = sig[0, 0] * sig[1, 1]
F[p] = ti.Matrix.identity(ti.f32, 2) * ti.sqrt(J)
affine += -4 * dt * (dx_inv ** 2) * vol_p * E * (J - 1) * ti.Matrix.identity(ti.f32, 2)
elif material[p] == 1:
J = sig[0, 0] * sig[1, 1]
h = 0.3
mu, la = mu_0 * h, lambda_0 * h
stress = 2 * mu * (F[p] - U @ V.transpose()) @ F[p].transpose() + la * (J - 1) * J * ti.Matrix.identity(ti.f32, 2)
affine += -4 * dt * (dx_inv ** 2) * vol_p * stress
elif material[p] == 2:
h = max(0.1, min(5, ti.exp(10 * (1.0 - Jp[p])))) # Hardening coefficient: snow gets harder when compressed
mu, la = mu_0 * h, lambda_0 * h
J = 1.0
for d in ti.static(range(2)):
new_sig = min(max(sig[d, d], 1 - 2.5e-2), 1 + 4.5e-3) # Plasticity
Jp[p] *= sig[d, d] / new_sig
sig[d, d] = new_sig
J *= new_sig
F[p] = U @ sig @ V.transpose()
stress = 2 * mu * (F[p] - U @ V.transpose()) @ F[p].transpose() + la * (J - 1) * J * ti.Matrix.identity(ti.f32, 2)
affine += -4 * dt * (dx_inv ** 2) * vol_p * stress
for i, j in ti.static(ti.ndrange(3, 3)):
offset = ti.Vector([i, j])
k = w[i].x * w[j].y
dpos = (offset.cast(float) - local) * dx
v_grid[base + offset] += k * (m_p * v[p] + affine @ dpos + m_p * f[p])
m_grid[base + offset] += k * m_p
@ti.kernel
def grid_op():
for i, j in v_grid:
I = ti.Vector([i, j])
if m_grid[I] <= 0:
continue
v_grid[I] = v_grid[I] / m_grid[I] + gravity * dt
if ti.static(bc_mode) == 0: # sticky
if i < bound or i >= n_grid - bound or j < bound or j >= n_grid - bound: v_grid[I] = [0, 0]
elif ti.static(bc_mode) == 1: # slip
if i < bound or i >= n_grid - bound: v_grid[I].x = 0
if j < bound or j >= n_grid - bound: v_grid[I].y = 0
elif ti.static(bc_mode) == 2: # separate
if i < bound and v_grid[I].x < 0: v_grid[I].x = 0
if i >= n_grid - bound and v_grid[I].x > 0: v_grid[I].x = 0
if j < bound and v_grid[I].y < 0: v_grid[I].y = 0
if j >= n_grid - bound and v_grid[I].y > 0: v_grid[I].y = 0
@ti.kernel
def g2p():
for p in x:
base = (x[p] * dx_inv - 0.5).cast(int)
local = x[p] * dx_inv - base
w = [0.5 * (1.5 - local) ** 2, 0.75 - (local - 1) ** 2, 0.5 * (local - 0.5) ** 2]
new_v = ti.Vector.zero(ti.f32, 2)
new_C = ti.Matrix.zero(ti.f32, 2, 2)
for i, j in ti.static(ti.ndrange(3, 3)):
k = w[i].x * w[j].y
offset = ti.Vector([i, j])
dpos = offset.cast(float) - local # actually dpos / dx
new_v += k * v_grid[base + offset]
new_C += k * 4 * dx_inv * v_grid[base + offset].outer_product(dpos)
x[p] += dt * new_v
v[p] = new_v
C[p] = new_C
def substep():
v_grid.fill(0)
m_grid.fill(0)
f.fill(0)
get_force()
p2g()
grid_op()
g2p()
def main():
gui = ti.GUI('trivial mpm with lagrangian force', res = (512, 512), background_color = 0x112F41)
result_dir = "./results"
#video_manager = ti.VideoManager(output_dir=result_dir, framerate=24, automatic_build=False)
init()
breakflag = False
while gui.running:
for e in gui.get_events(ti.GUI.PRESS):
if e.key in [ti.GUI.ESCAPE, ti.GUI.EXIT]: breakflag = True
elif e.key == 'r': init()
elif e.key == 'g':
for subframe in range(n_subframes):
substep()
if breakflag: break
for subframe in range(n_subframes):
substep()
gui.circles(x.to_numpy()[0: n_mesh], radius = 1, color = 0xF2B134)
gui.circles(x.to_numpy()[n_mesh: n_mesh + n_each], color = 0x068587)
gui.circles(x.to_numpy()[n_mesh + n_each: n_mesh + n_each * 2], color = 0xED553B)
gui.circles(x.to_numpy()[n_mesh + n_each * 2: n_particles], color = 0xEEEEF0)
#video_manager.write_frame(gui.get_image())
gui.show()
#video_manager.make_video(gif = True, mp4 = True)
if __name__ == '__main__': main()