板上已经有其他同学写过了格式各样炫酷的流体求解器，作为专业研究流体力学的 
，写了一个计算流体力学视角的求解器。相比图形学中的流体仿真，工业上的流体仿真对准确性的要求更高一些，因而很难做到real-time simulation。这里的求解器采用了Lattice Boltzmann方法，在taichi的cuda backend下居然能跑到54FPS （GTX 960）。
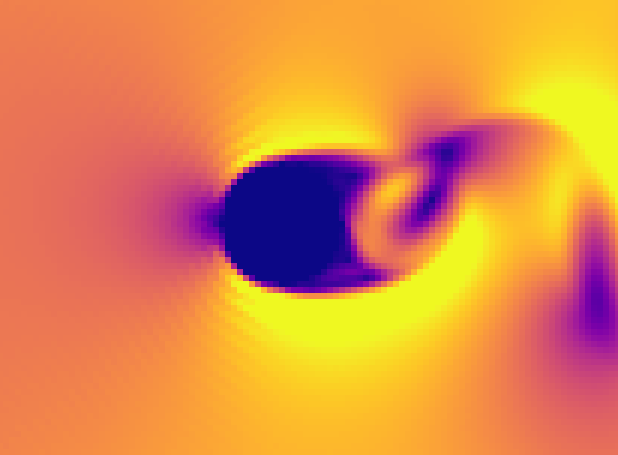
程序提供了两个科普算例，一个是卡门涡街（卡门指的是钱学森的导师von Karman）。卡门涡街是流体流过钝体时产生周期性的尾涡脱落的有趣现象，模拟结果如下：
代码如下：
import taichi as ti
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
ti.init(arch=ti.gpu)
@ti.data_oriented
class lbm_solver:
def __init__(self,
nx, # domain size
ny,
niu, # viscosity of fluid
bc_type, # [left,top,right,bottom] boundary conditions: 0 -> Dirichlet ; 1 -> Neumann
bc_value, # if bc_type = 0, we need to specify the velocity in bc_value
cy = 0, # whether to place a cylindrical obstacle
cy_para = [0.0, 0.0, 0.0], # location and radius of the cylinder
steps = 60000): # total steps to run
self.nx = nx # by convention, dx = dy = dt = 1.0 (lattice units)
self.ny = ny
self.niu = niu
self.tau = 3.0 * niu + 0.5
self.inv_tau = 1.0 / self.tau
self.rho = ti.var(dt=ti.f32, shape=(nx, ny))
self.vel = ti.Vector(2, dt=ti.f32, shape=(nx, ny))
self.mask = ti.var(dt=ti.f32, shape=(nx, ny))
self.display_var = ti.var(dt=ti.f32, shape=(nx, ny))
self.f_old = ti.Vector(9, dt=ti.f32, shape=(nx, ny))
self.f_new = ti.Vector(9, dt=ti.f32, shape=(nx, ny))
self.w = ti.var(dt=ti.f32, shape=9)
self.e = ti.var(dt=ti.i32, shape=(9, 2))
self.bc_type = ti.var(dt=ti.i32, shape=4)
self.bc_value = ti.var(dt=ti.f32, shape=(4, 2))
self.cy = cy
self.cy_para = ti.var(dt=ti.f32, shape=3)
self.bc_type.from_numpy(np.array(bc_type, dtype=np.int32))
self.bc_value.from_numpy(np.array(bc_value, dtype=np.float32))
self.cy_para.from_numpy(np.array(cy_para, dtype=np.float32))
self.steps = steps
arr = np.array([ 4.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 9.0, 1.0 / 36.0,
1.0 / 36.0, 1.0 / 36.0, 1.0 / 36.0], dtype=np.float32)
self.w.from_numpy(arr)
arr = np.array([[0, 0], [1, 0], [0, 1], [-1, 0], [0, -1], [1, 1],
[-1, 1], [-1, -1], [1, -1]], dtype=np.int32)
self.e.from_numpy(arr)
@ti.func # compute equilibrium distribution function
def f_eq(self, i, j, k):
eu = ti.cast(self.e[k, 0], ti.f32) * self.vel[i, j][0] + ti.cast(self.e[k, 1],
ti.f32) * self.vel[i, j][1]
uv = self.vel[i, j][0]**2.0 + self.vel[i, j][1]**2.0
return self.w[k] * self.rho[i, j] * (1.0 + 3.0 * eu + 4.5 * eu**2 - 1.5 * uv)
@ti.kernel
def init(self):
for i, j in self.rho:
self.vel[i, j][0] = 0.0
self.vel[i, j][1] = 0.0
self.rho[i, j] = 1.0
self.mask[i, j] = 0.0
for k in ti.static(range(9)):
self.f_new[i, j][k] = self.f_eq(i, j, k)
self.f_old[i, j][k] = self.f_new[i, j][k]
if(self.cy==1):
if ((ti.cast(i, ti.f32) - self.cy_para[0])**2.0 + (ti.cast(j, ti.f32)
- self.cy_para[1])**2.0 <= self.cy_para[2]**2.0):
self.mask[i, j] = 1.0
@ti.kernel
def collide_and_stream(self): # lbm core equation
for i, j in ti.ndrange((1, self.nx - 1), (1, self.ny - 1)):
for k in ti.static(range(9)):
ip = i - self.e[k, 0]
jp = j - self.e[k, 1]
self.f_new[i,j][k] = (1.0-self.inv_tau)*self.f_old[ip,jp][k] + \
self.f_eq(ip,jp,k)*self.inv_tau
@ti.kernel
def update_macro_var(self): # compute rho u v
for i, j in ti.ndrange((1, self.nx - 1), (1, self.ny - 1)):
self.rho[i, j] = 0.0
self.vel[i, j][0] = 0.0
self.vel[i, j][1] = 0.0
for k in ti.static(range(9)):
self.f_old[i, j][k] = self.f_new[i, j][k]
self.rho[i, j] += self.f_new[i, j][k]
self.vel[i, j][0] += (ti.cast(self.e[k, 0], ti.f32) *
self.f_new[i, j][k])
self.vel[i, j][1] += (ti.cast(self.e[k, 1], ti.f32) *
self.f_new[i, j][k])
self.vel[i, j][0] /= self.rho[i, j]
self.vel[i, j][1] /= self.rho[i, j]
@ti.kernel
def apply_bc(self): # impose boundary conditions
# left and right
for j in ti.ndrange(1, self.ny - 1):
# left: dr = 0; ibc = 0; jbc = j; inb = 1; jnb = j
self.apply_bc_core(1, 0, 0, j, 1, j)
# right: dr = 2; ibc = nx-1; jbc = j; inb = nx-2; jnb = j
self.apply_bc_core(1, 2, self.nx - 1, j, self.nx - 2, j)
# top and bottom
for i in ti.ndrange(self.nx):
# top: dr = 1; ibc = i; jbc = ny-1; inb = i; jnb = ny-2
self.apply_bc_core(1, 1, i, self.ny - 1, i, self.ny - 2)
# bottom: dr = 3; ibc = i; jbc = 0; inb = i; jnb = 1
self.apply_bc_core(1, 3, i, 0, i, 1)
# cylindrical obstacle
# Note: for cuda backend, putting 'if statement' inside loops can be much faster!
for i, j in ti.ndrange(self.nx, self.ny):
if (self.cy == 1 and self.mask[i, j] == 1):
self.vel[i, j][0] = 0.0 # velocity is zero at solid boundary
self.vel[i, j][1] = 0.0
inb = 0
jnb = 0
if (ti.cast(i,ti.f32) >= self.cy_para[0]):
inb = i + 1
else:
inb = i - 1
if (ti.cast(j,ti.f32) >= self.cy_para[1]):
jnb = j + 1
else:
jnb = j - 1
self.apply_bc_core(0, 0, i, j, inb, jnb)
@ti.func
def apply_bc_core(self, outer, dr, ibc, jbc, inb, jnb):
if (outer == 1): # handle outer boundary
if (self.bc_type[dr] == 0):
self.vel[ibc, jbc][0] = self.bc_value[dr, 0]
self.vel[ibc, jbc][1] = self.bc_value[dr, 1]
elif (self.bc_type[dr] == 1):
self.vel[ibc, jbc][0] = self.vel[inb, jnb][0]
self.vel[ibc, jbc][1] = self.vel[inb, jnb][1]
self.rho[ibc, jbc] = self.rho[inb, jnb]
for k in ti.static(range(9)):
self.f_old[ibc,jbc][k] = self.f_eq(ibc,jbc,k) - self.f_eq(inb,jnb,k) + \
self.f_old[inb,jnb][k]
@ti.kernel
def get_display_var(self, flg: ti.i32):
if (flg == 0): # get velocity magnitude
for i, j in ti.ndrange(self.nx, self.ny):
self.display_var[i, j] = ti.sqrt(self.vel[i, j][0]**2.0 +
self.vel[i, j][1]**2.0)
elif (flg == 1): # get x-direction component only
for i, j in ti.ndrange(self.nx, self.ny):
self.display_var[i, j] = self.vel[i, j][0]
def solve(self):
gui = ti.GUI('lbm solver', (self.nx, self.ny))
self.init()
for i in range(self.steps):
self.collide_and_stream()
self.update_macro_var()
self.apply_bc()
self.get_display_var(0)
img = cm.plasma(self.display_var.to_numpy() / 0.15)
gui.set_image(img)
gui.show()
if (i % 1000 == 0):
print('Step: {:}'.format(i))
# ti.imwrite((img[:,:,0:3]*255).astype(np.uint8), 'fig/karman_'+str(i).zfill(6)+'.png')
def pass_to_py(self):
self.get_display_var(1)
return self.display_var.to_numpy()
if __name__ == '__main__':
flow_case = 0
if (flow_case == 0): # von Karman vortex street: Re = U*D/niu = 200
lbm = lbm_solver(401, 101, 0.005, [0, 0, 1, 0],
[[0.1, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0]],
1,[80.0, 50.0, 10.0])
lbm.solve()
elif (flow_case == 1): # lid-driven cavity flow: Re = U*L/niu = 1000
lbm = lbm_solver(256, 256, 0.0255, [0, 0, 0, 0],
[[0.0, 0.0], [0.1, 0.0], [0.0, 0.0], [0.0, 0.0]])
lbm.solve()
# compare with literature results
y_ref, u_ref = np.loadtxt('data/ghia1982.dat', unpack=True, skiprows=2, usecols=(0, 2))
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(4, 3), dpi=200)
axes.plot(np.linspace(0, 1.0, 256), lbm.pass_to_py()[256 // 2, :] / 0.1, 'b-', label='LBM')
axes.plot(y_ref, u_ref, 'rs', label='Ghia et al. 1982')
axes.legend()
axes.set_xlabel(r'Y')
axes.set_ylabel(r'U')
plt.tight_layout()
plt.show()
新人只能发一张图 ，详细一点的介绍见LBM_Taichi。
，果然大佬是没有知识盲区的。现在程序里的曲面边界算法太糙了，还容易被各种反射波干扰，画出的vorticity没有这么干净漂亮，后续再找个好点的算法算算看 
