Homework -1: 自制Taichi的cg和numpy比较

GAMES201 高级物理引擎课程专区
#1

做了一个Homework -1（负1）。。意图很简单就是定量地比较一下Taichi下自制的简单linear solver和numpy的求解器相比性能如何。

一共写了两个脚本，一个用来测试Taichi，一个用来numpy，互不干扰。代码存放在这里。

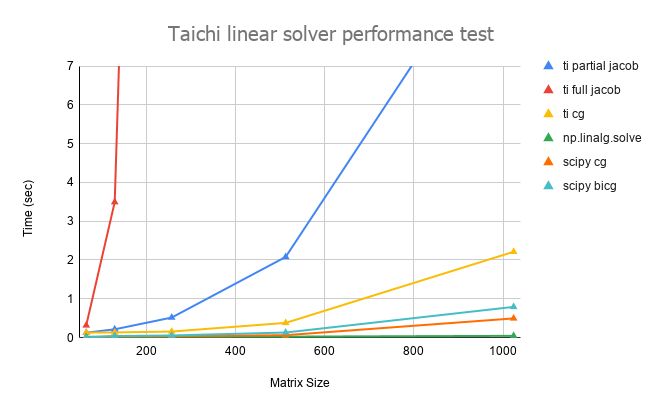
结果直接上图：
Taichi linear solver performance test

计算内容和计算方法：

首先求解的是Ax = b这个线性方程组的解x。A是一个如下的矩阵（尺寸是可变的）：
mat_A
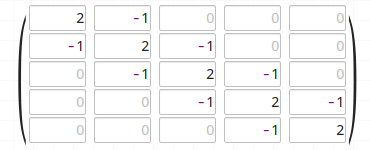
b的第一个元素是100，其余元素都是0。

各个曲线分别代表各个求解器在不同矩阵尺寸下求解的时间：

  1. ti full jacobian：这个就是在课程里老师用的最简单的Jacobian求解器
  2. ti partial jacobian：这个是针对A的三对角形状，在每个Jacobian循环中仅访问每行中不是0的3个元素
  3. ti cg：用Taichi写的Conjugate gradient求解器
  4. np.linalg.solve：numpy linaly包里的线性求解器，应该是direct method?
  5. scipy cg：scipy的Conjugate gradient求解器
  6. scipy bicg：scipy的Bi-Conjugate gradient求解器

一些观察和结论：

  1. Jacobian虽然很不堪，但是求解三对角的时候省略掉所有0元素（相当于手动稀疏化了？），求解还是会快很多
  2. 最简单的Conjugate gradient实现很容易，但是性能也比较差强人意，关键是仅仅在A是正定对称的情况下才有解
  3. Scipy的Conjugate gradient还是要比手写naive版本的Taichi快将近一倍
  4. Numpy的solve真的很快，不知道内部是什么实现，难道会自动TDMA？

一些奇怪的现象：

  1. 随机数初始化在Taichi里好像是有问题的，如果把如下的函数放到kernel里，那么其实只会产生一个随机数，并把这个数用到所有的初始化里，具体大家可以试一试。
# @ti.kernel 这里如果做成kernel就会产生不完全随机现象
def init_rand():
    for i in range(n):
        for j in range(n):
            A[i, j] = random.random() - 0.5
        A[i, i] += n * 0.1
        b[i] = random.random() * 100
  1. 在检查残差的时候，下面这个函数也不可以放到Taichi scope，否则会返回一些奇怪的值，而且反复执行每次结果都会不一样？
# @ti.kernel
def check_sol() -> ti.f64:
    res = 0.0
    r = 0.0
    for i in range(n):
        r = b[i]
        for j in range(n):
            r -= A[i, j] * x[j]
        res += r * r
    return res

下一步的任务：

  1. 在Taichi里实现bicg和bicgstab，使其可以用在不对称的A矩阵上
  2. 优化Taichi里的Conjugate gradient，比如说针对三对角的矩阵可以在点乘的时候手动省略0元素？
  3. 尝试在Taichi里用稀疏矩阵，观察性能的变化（有人能教我具体怎么做吗？）

代码写得都很水，大家如果有什么改进意见都请告诉我，也可以在Github直接评论或者PR！谢谢大家！

3 个赞
#2

我自己也写了下 “手工自制”jacobian，被numpy吊着打… 不知道可不可以在kernel里用numpy求解…

#3 
# @ti.kernel
def check_sol() -> ti.f64:
    res = 0.0
    r = 0.0  # 错误！第一次出现是全局，所以 r 变成全局变量了！
    for i in range(n):
        r = b[i]
        for j in range(n):
            r -= A[i, j] * x[j]
        res += r * r
    return res

应该改成：

@ti.kernel
def check_sol() -> ti.f64:
    res = 0.0
    for i in range(n):
        r = b[i]  # 第一次出现是局部，所以 r 是局部变量
        for j in range(n):
            r -= A[i, j] * x[j]
        res += r * r
    return res
1 个赞
#4

这是因为 @ti.kernel 里的 for 循环会并行执行的原因。
注：最新版本中可以使用 ti.init(arch=ti.cc) 禁止一切并行 for，从而和 Python scope 一致。

# @ti.kernel
def check_sol() -> ti.f64:
    res = 0.0
    r = 0.0  # 错误！第一次出现是全局，所以 r 变成全局变量了！
    for i in range(n):
        r = b[i]
        for j in range(n):
            r -= A[i, j] * x[j]
        res += r * r
    return res

应该改成：

@ti.kernel
def check_sol() -> ti.f64:
    res = 0.0
    for i in range(n):
        r = b[i]  # 第一次出现是局部，所以 r 是局部变量
        for j in range(n):
            r -= A[i, j] * x[j]
        res += r * r
    return res

除此以外还有：

# @ti.kernel
def init_rand():
    for i in range(n):
        for j in range(n):
            A[i, j] = random.random() - 0.5
        A[i, i] += n * 0.1  # 和上一个赋值的时序可能颠倒（另一个线程也在写入 A[i, i]）
        b[i] = random.random() * 100

应该改成

@ti.kernel
def init_rand():
    for i in range(n):
        for j in range(n):
            A[i, j] = random.random() - 0.5
    for i in range(n):  # 保证第一个赋值全部完成后才操作 A[i, j]
        A[i, i] += n * 0.1
        b[i] = random.random() * 100
1 个赞
#5

init_rand()那里应该是需要将random替换为ti.random，测试代码见下

import random
import taichi as ti
ti.init(ti.cpu)
@ti.data_oriented
class DummyD:
    def __init__(self):
        self.a = ti.field(ti.f64, shape=())
    @ti.kernel
    def calculate0(self):
        self.a[None] = random.random()
    @ti.kernel
    def calculate1(self):
        self.a[None] = ti.random(ti.f64)
z0 = DummyD()
for _ in range(3):
    z0.calculate0()
    print(z0.a[None]) #always same
for _ in range(3):
    z0.calculate1()
    print(z0.a[None]) #different every time
#6

请问homework1是在哪里呀？