实现了基于 Neohookean 弹性模型的 3D 线性有限元,并对比了三种数值方法:1.显式时间积分;隐式时间积分(2. Jacobi方法求解,3.共轭梯度法求解)
一周前就写完了,这几天忙着入职和租房,一直没有时间写分析……今天抽时间写了出来,顺便渲染了结果便于对比。
Introduction
An implementation of 3D linear FEM based on Neohookean elasticity model (No damping force).
Simulation Results



Using Explicit, Jacobi and CG method respectively (Rendered by Blender).
Analysis
For Explicit method, there is no constraints between nodes when updating, so the system explodes if time step or Young’s modulus is large.
For Jacobi method, the convergence is determined by the spectral radius \rho of the matrix -D^{-1}(L+U) , Jacobi method converges if and only if \rho is less than 1.
For CG method, the system always converges since the coefficient matrix A is positive definite for (solid) FEM problems.
Same Scene
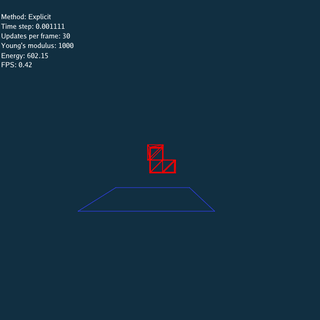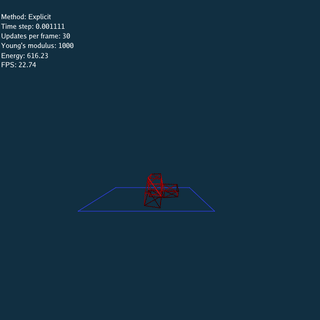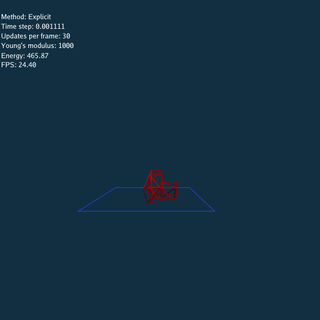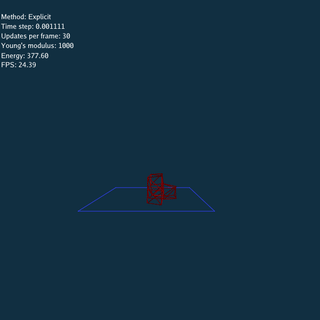
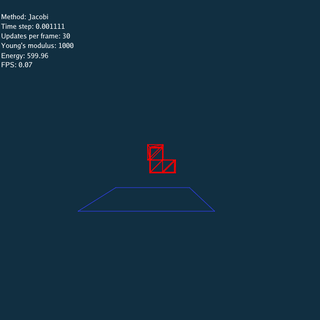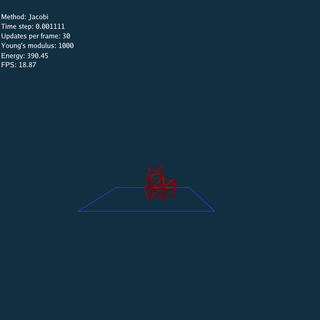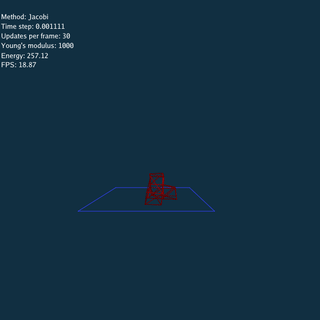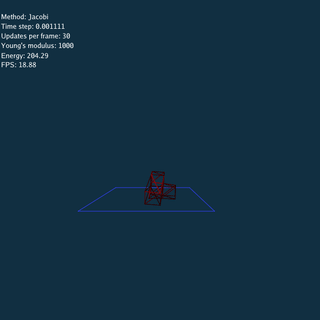

Explicit and Jacobi method have to update many times using a small time step at each frame.
\rho = 0.0036
Large Time Step
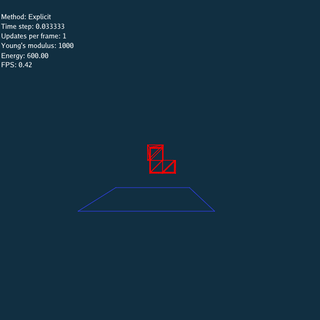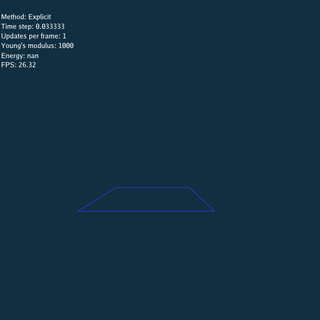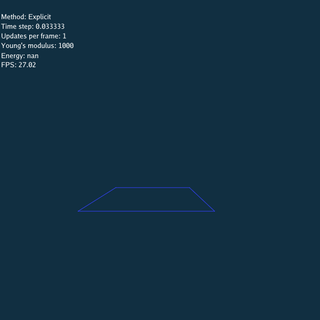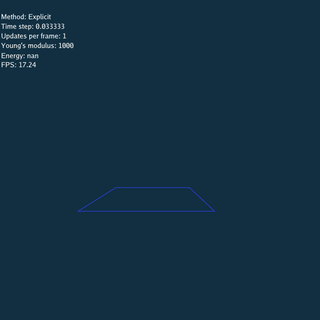
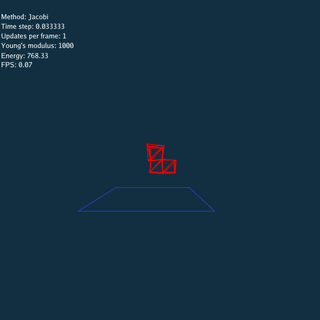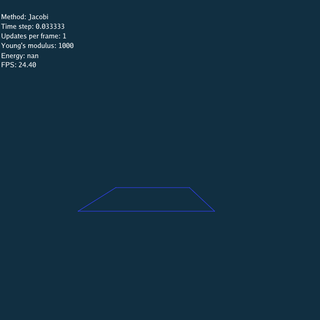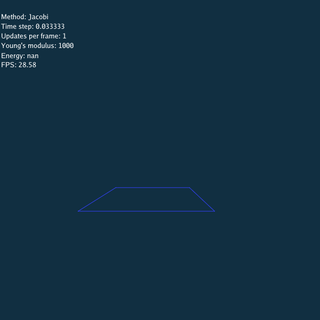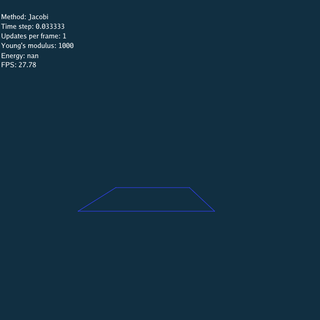

\rho = 1.09
Large Young’s Modulus
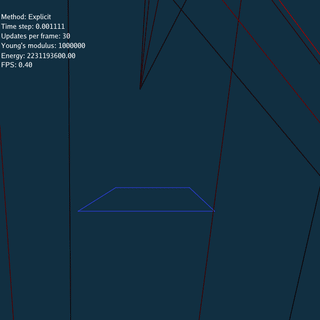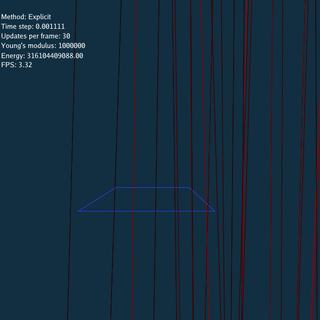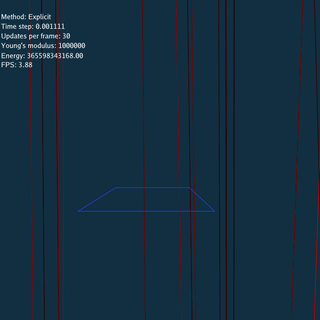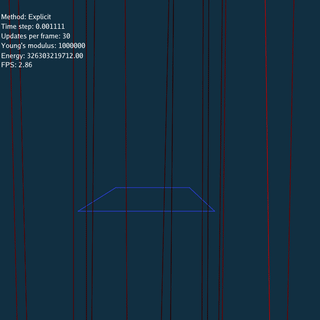

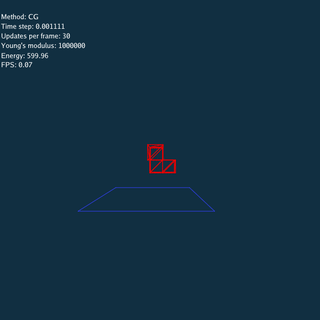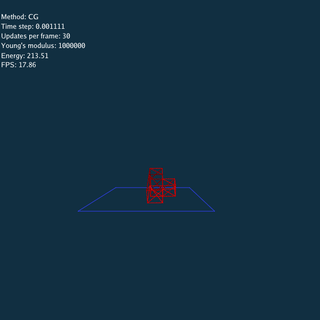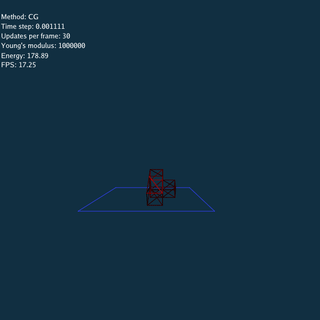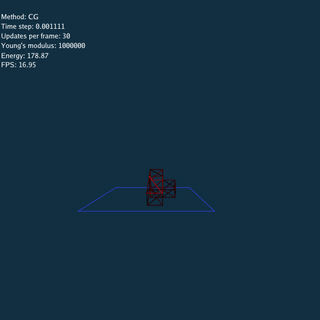
\rho = 1.13
Problems of Conjugate Gradient Method

- Object rotates slowly when time step is large.
This problem is caused by the lack of damping force, add damping force to object can avoid this problem.
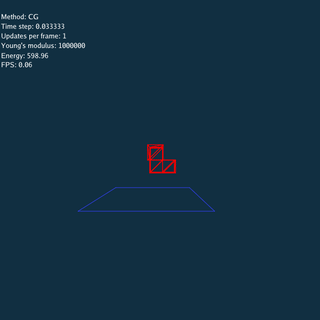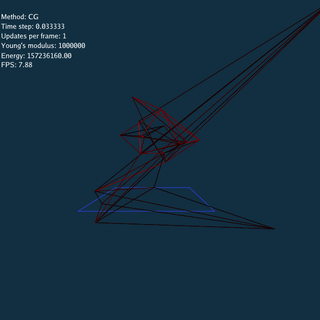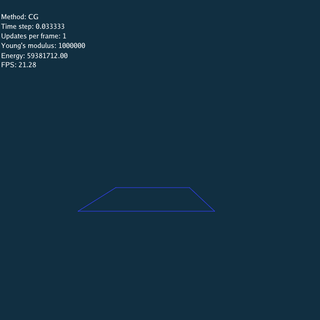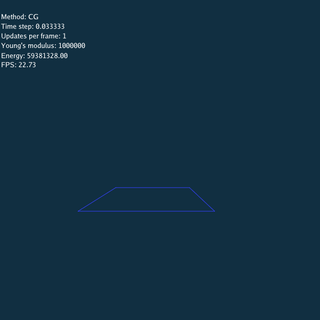
- CG doesn’t converge when both time step and Young’s modulus are large.
I still don’t know why CG doesn’t converge in this condition, I guess this is caused by numerical accuracy.