感谢胡老师提供的taichi编程语言,fractal的demo让我很有兴趣去做点小修改。
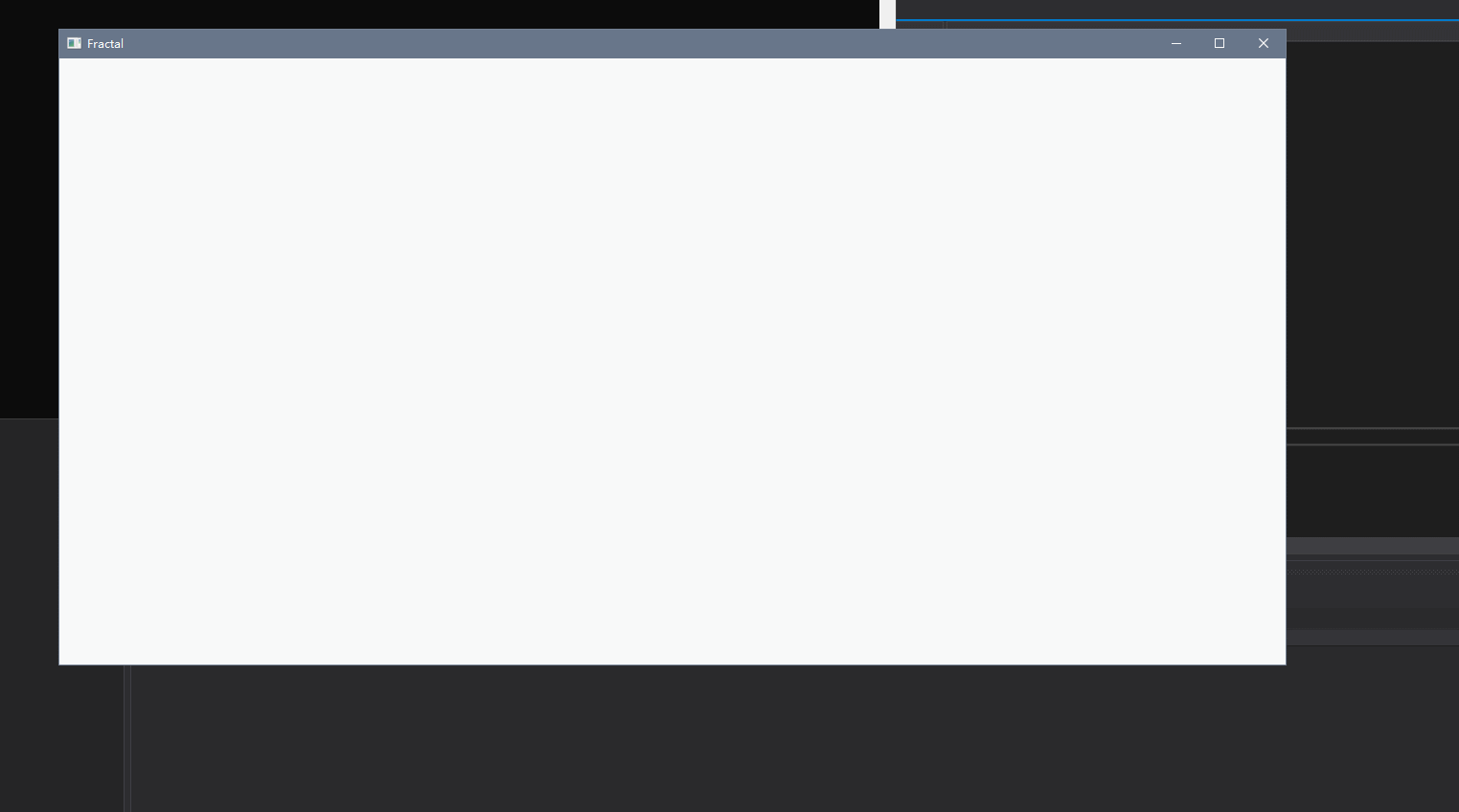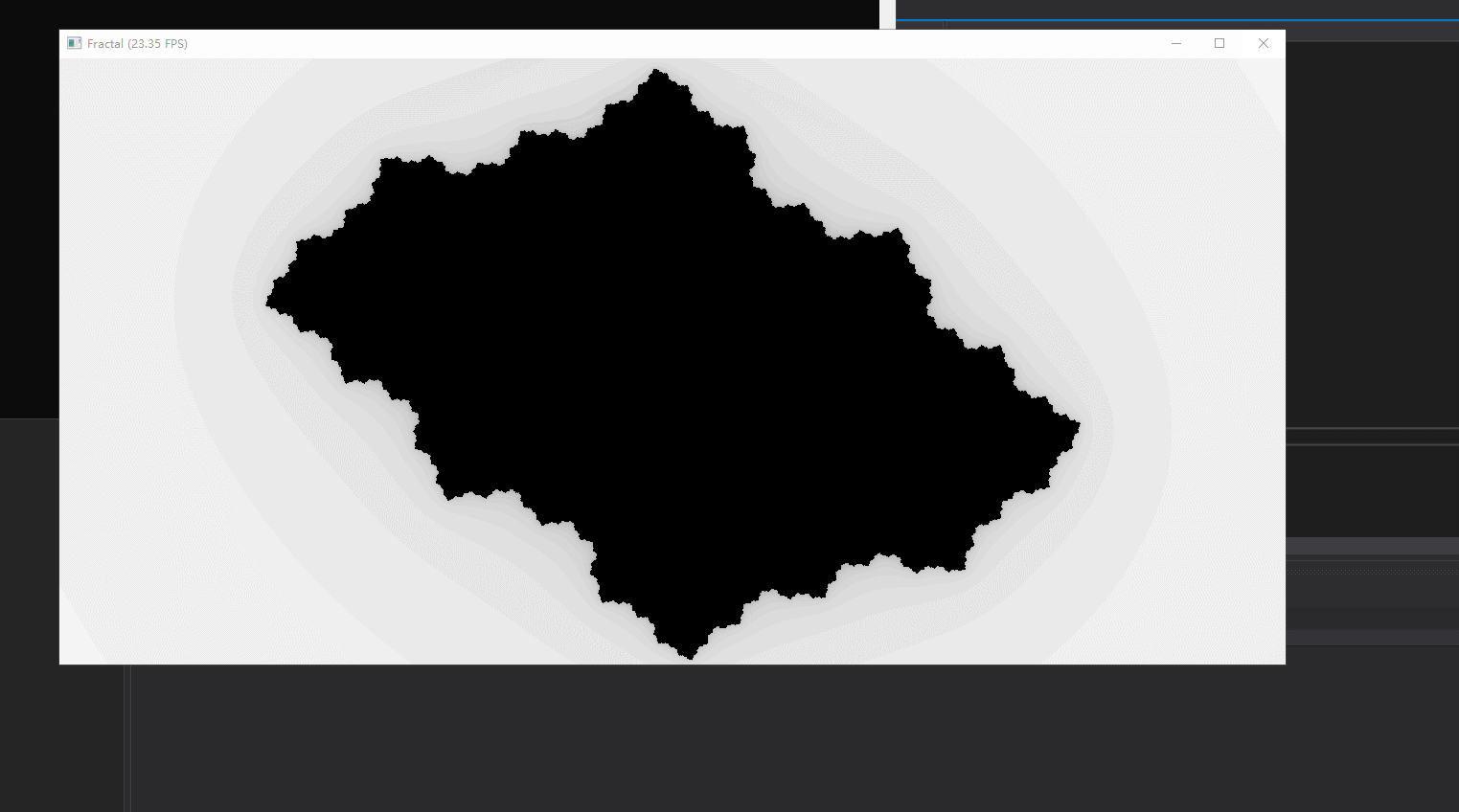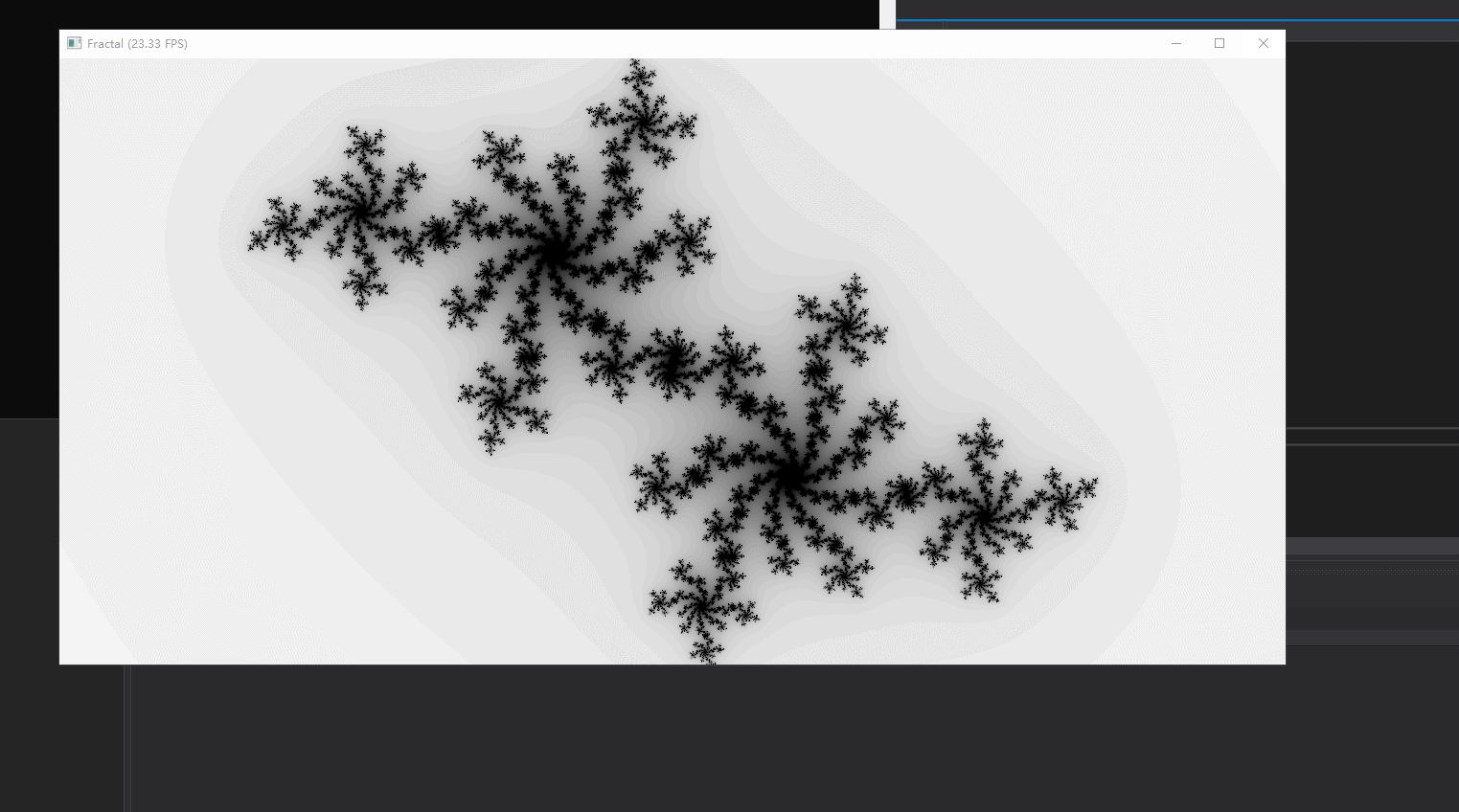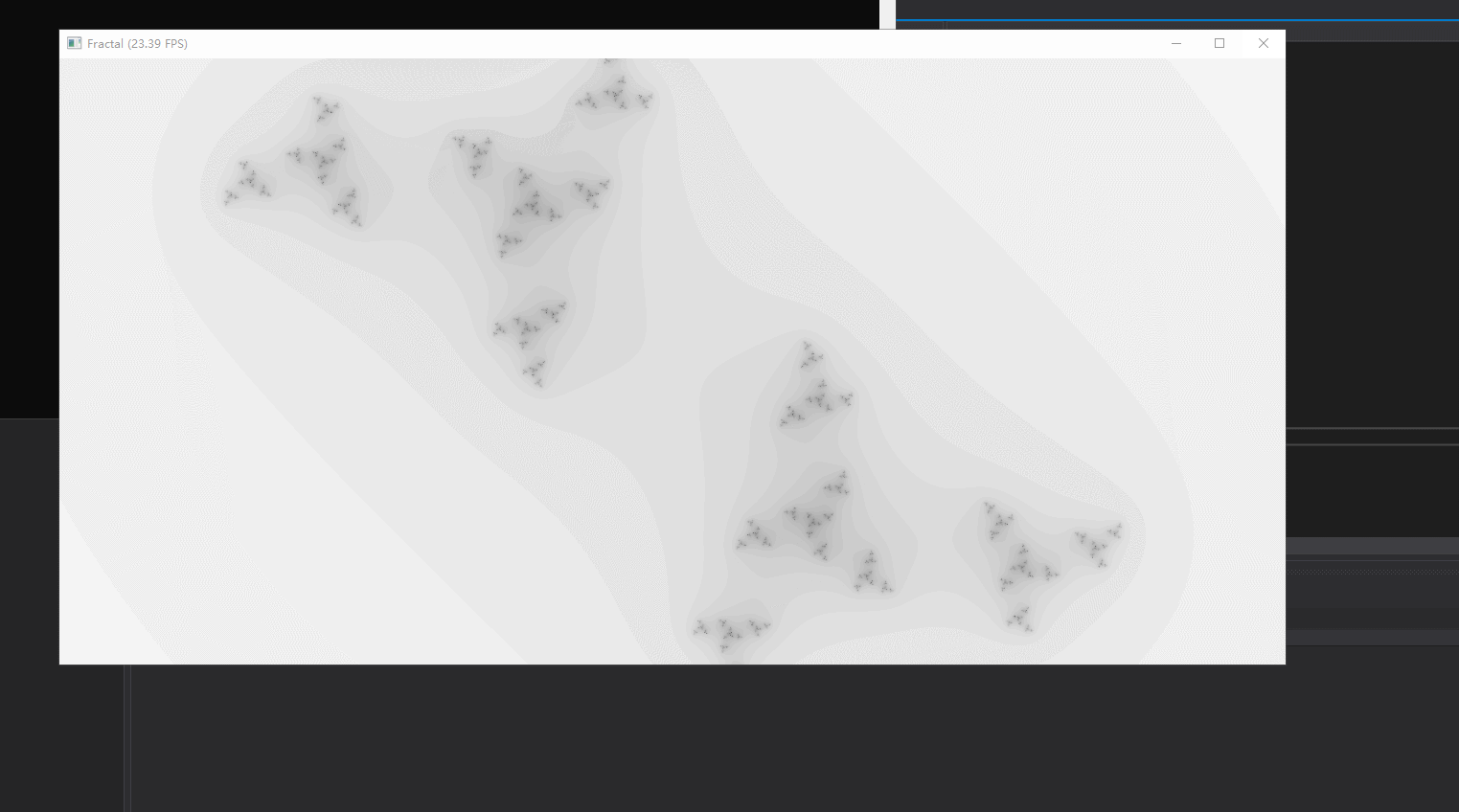
先简单解释下fractal demo中的图像含义。它是 z_{t+1} = z_t^n + c 中z的收敛范围,其中z和c都是复数。
例如 z_{t+1} = z_t^2 - 0.8 中
假如
z_0 = 0,z_1 = -0.8, z_2 = -0.16, z_3 = -0.7744, 由此可见,z = 0 会收敛,因此会显示在图中。
对demo做了简单的修改使得它可以用任意整数做z的幂。
import taichi as ti
ti.init(arch=ti.gpu)
n = 320
pixels = ti.var(dt=ti.f32, shape=(n * 2, n))
@ti.func
def complex_power(z, power: ti.i32):
r = ti.sqrt(z[0]**2 + z[1]**2)
theta = ti.atan2(z[1], z[0])
return ti.Vector([r**power * ti.cos(power*theta), r**power * ti.sin(power*theta)])
@ti.kernel
def paint(t: ti.f32, power: ti.i32):
for i, j in pixels: # Parallized over all pixels
freq = 1.0 / power
c = ti.Vector([0.7885 * ti.cos(freq*t), 0.7885 * ti.sin(freq*t)])
z = ti.Vector([i / n - 1, j / n - 0.5]) * 2
iterations = 0
while z.norm() < 20 and iterations < 50:
z = complex_power(z, power) + c
iterations += 1
pixels[i, j] = 1 - iterations * 0.02
power = eval(input("Power of z -> "))
gui = ti.GUI("Julia Set", res=(n * 2, n))
for i in range(1000000):
paint(i * 0.03, power)
gui.set_image(pixels)
gui.show()
比如当 n = 3 的时候:
n = 5 的时候:
由于c的实数部分也写成了关于t的函数,所以会出现式子不收敛的情况,对应的就是没有黑色pixel的情况。同样也会有一些奇怪的图形产生:
大家也可以随意对c进行修改,会有不一样的效果 ![]()
再次感谢胡老师带来的欢乐。重新回到了小学二年级 ![]()
关于fractal以及一些拓展,可以看看 这个方程会改变你的世界观_哔哩哔哩_bilibili