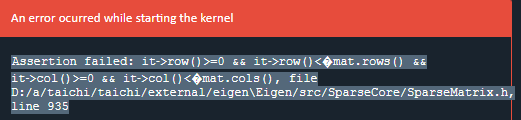
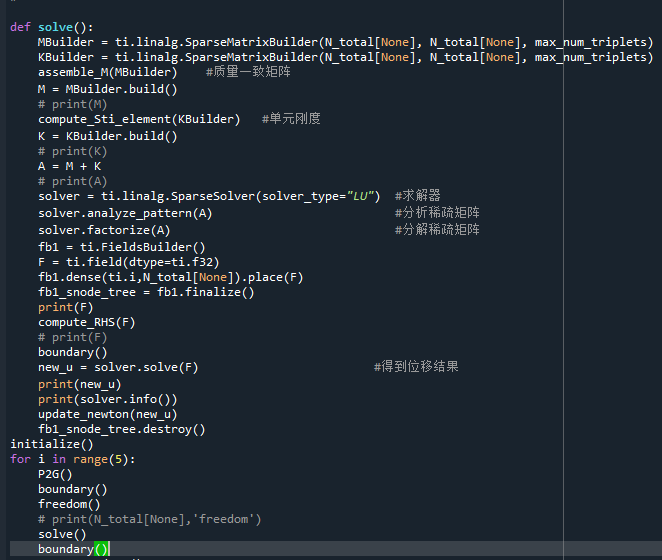
这个我的代码,应该就是稀疏矩阵那个shape每一步不一样导致的问题。稀疏矩阵是不是也能像field一样每一步.destroy()?
期待您的解答。
import taichi as ti #引入taichi模块的同时为该模块取名为ti
ti.init(arch=ti.cpu,default_fp=ti.f32,default_ip=ti.i32)
quality = 1
n_particles, n_grid= 200 * quality **2, 50 * quality
dx = 1
inv_dx = 1/dx
dt = 1e-3 / quality
p_vol, p_rho = (dx)**2, 1000
p_mass = p_vol * p_rho/4
E, nu = 1.0e6, 0.0
G=E/(2*(1+nu))
K_modulus=E/(3*(1-2*nu)) #体积模量
gravity = ti.Vector([0,-9.8]) #每个粒子的重力
x = ti.Vector.field(2, dtype=ti.f32, shape=n_particles) # position
ini_x = ti.Vector.field(2, dtype=ti.f32, shape=n_particles)
grid_u = ti.Vector.field(2, dtype=ti.f32, shape=(n_grid, n_grid))
grid_fext = ti.Vector.field(2, dtype=ti.f32, shape=(n_grid, n_grid))
grid_m = ti.field(dtype=ti.f32, shape=(n_grid, n_grid)) #grid node mass
base = ti.Vector.field(2,dtype = ti.f32, shape = n_particles) #粒子坐标整数值
fx = ti.Vector.field(2,dtype = ti.f32, shape = n_particles) #粒子坐标小数值(偏移整数坐标的量)
w = ti.Matrix.field(2,2,dtype = ti.f32, shape = n_particles) #形函数
de_w=ti.Matrix.field(2,2,dtype = ti.f32, shape = n_particles) #形函数导数
m_rho = ti.field(dtype = ti.f32, shape = n_particles) #粒子密度
extract = ti.Vector.field(6, dtype=ti.f32,shape=n_particles)
#-----------------------------------------------------------------------------------
max_num_triplets = 10000000
#-----------------------------------------------------------------------------------
N_total = ti.field(dtype=ti.i32,shape=())
number_v = ti.field(dtype=ti.i32,shape=(n_grid, n_grid))
@ti.kernel
def initialize(): # 初始条件,位置、速度、密度
for i in range(n_particles):
x[i] = [i%2*0.5+1.25,i//2*0.5+0.25]
ini_x[i] = [i%2*0.5+1.25,i//2*0.5+0.25]
m_rho[i] = 1000
@ti.kernel
def P2G():
for i, j in grid_m: #清空网格上速度、质量信息
grid_m[i, j] = 0.0
grid_u[i, j] = [0.0, 0.0]
for p in range(n_particles) :
base[p] = (x[p] * inv_dx).cast(ti.i32) #base为基础下标 x的第p个粒子 每个数×inv_dx,然后把全转成整数
fx[p] = x[p] * inv_dx - base[p].cast(ti.f32) #fx表示粒子偏移网格位置 即该粒子距离格子左下角的局部坐标
w0=[1-fx[p],fx[p]] #形函数
for i,j in ti.static(ti.ndrange(2,2)): #组装形函数矩阵
w[p][i,j]=w0[i][j]
de_w = [-1,1] #形函数导数
for i,j in ti.static(ti.ndrange(2,2)): #遍历相邻四个格子
offset=ti.Vector([i,j])
weight = w[p][i,0] * w[p][j,1] #权重比例
grid_m[base[p] + offset] += weight * p_mass #网格点上的质量信息
@ti.kernel
def assemble_M(A: ti.linalg.sparse_matrix_builder()): #组装稀疏质量矩阵
n_free = 0
for k in range(1):
for i,j in ti.ndrange(n_grid, n_grid):
if grid_m[i,j] > 0:
n_free += 1
ele_num = int(N_total[None]/2)
A[(n_free-1), (n_free-1)] += 4*grid_m[i,j]/(dt**2)
A[(n_free-1) + ele_num, (n_free-1) + ele_num] += 4*grid_m[i,j]/(dt**2)
else:
n_free += 0
@ti.kernel
def compute_RHS(v: ti.template()):
n_free = 0
for i,j in grid_m:
if grid_m[i,j] > 0:
grid_fext[i,j] += 1.0
for k in range(1):
for i,j in ti.ndrange(n_grid, n_grid):
if grid_m[i,j] > 0:
n_free += 1
ele_num = int(N_total[None]/2)
v[(n_free-1)] = 1.0
v[(n_free-1) + ele_num] = 2.0
else:
n_free += 0
@ti.kernel
def update_newton(new_u: ti.ext_arr()):
n_free = 0
for k in range(1):
for i,j in ti.ndrange(n_grid, n_grid):
if grid_m[i,j] > 0:
n_free += 1
ele_num = int(N_total[None]/2)
grid_u[i,j][0] = new_u[n_free-1]
grid_u[i,j][1] = new_u[(n_free-1) + ele_num]
else:
n_free += 0
grid_u[i,j][0] = 0.0
grid_u[i,j][1] = 0.0
def solve():
MBuilder = ti.linalg.SparseMatrixBuilder(N_total[None], N_total[None], max_num_triplets)
KBuilder = ti.linalg.SparseMatrixBuilder(N_total[None], N_total[None], max_num_triplets)
assemble_M(MBuilder) #质量一致矩阵
M = MBuilder.build()
A = M
# print(A)
solver = ti.linalg.SparseSolver(solver_type="LU") #求解器
solver.analyze_pattern(A) #分析稀疏矩阵
solver.factorize(A) #分解稀疏矩阵
fb2 = ti.FieldsBuilder()
F = ti.field(dtype=ti.f32)
fb2.dense(ti.i, N_total[None]).place(F)
fb2_snode_tree = fb2.finalize()
compute_RHS(F)
new_u = solver.solve(F) #得到位移结果
# print(solver.info())
update_newton(new_u)
fb2_snode_tree.destroy()
initialize()
for i in range(500):
P2G()
N_total[None] = 2*i
# print(N_total[None],'freedom')
solve()