流体的模拟仿真在影视特效,虚拟现实,工业设计中都有广泛的应用。研究如何精确模拟还原流体行为的学科,称为计算流体力学(Computational Fluid Dynamics)或者简称为 CFD。

影视作品《海洋奇缘》中的海浪流体仿真
随着 Taichi 社区中 CFD 相关的优秀项目越来越多,也有很多吃瓜的同学产生了这样的疑问:
Taichi 不是专门为图形学设计的语言吗?Taichi 可不可以被用来做高性能计算?Taichi 可以用来写计算流体力学的程序吗?作为“用 Taichi 开始的计算流体力学”系列博客的第一篇,本文就尝试解答一下上述疑问。

Taichi 社区中涌现的优秀流体仿真项目
目录
01 流体数值计算对计算语言的需求
02 Taichi 语言是否能应对流体计算的需求
03 在流体计算中 Taichi kernel 的应用
04 小结
01 流体数值计算对计算语言的需求
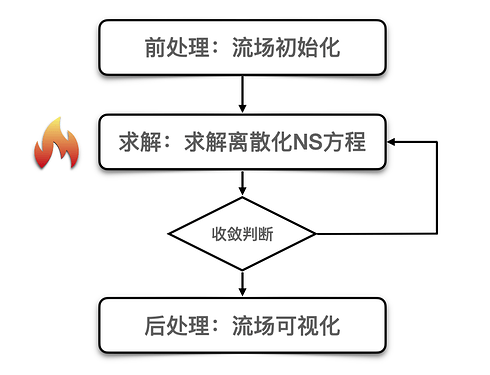
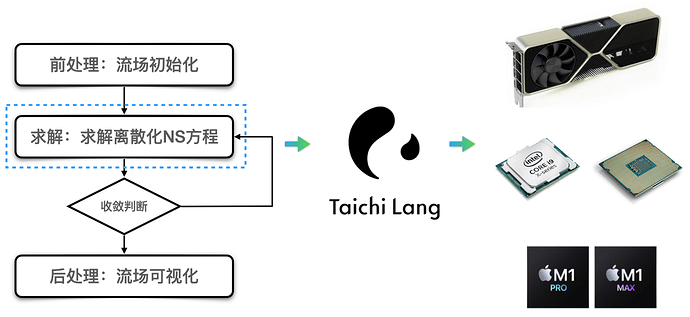
在回答 Taichi 能否用来做流体数值计算之前,我们先要回答:所谓的计算流体力学到底是一种什么样的计算?通常来说,流体力学的仿真计算会包含如下步骤:
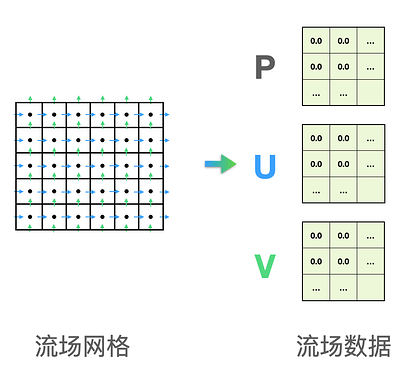
这其中,最耗费计算时间的无疑是流场的求解部分,同时这也是 Taichi 语言最擅长并行加速的部分。在前处理中,我们需要建立保存流场信息(例如速度分量 U 和 V,压力 P,密度等等)的数据结构(通常是 2 维或者 3 维的数组),并对它们的数值进行初始化。
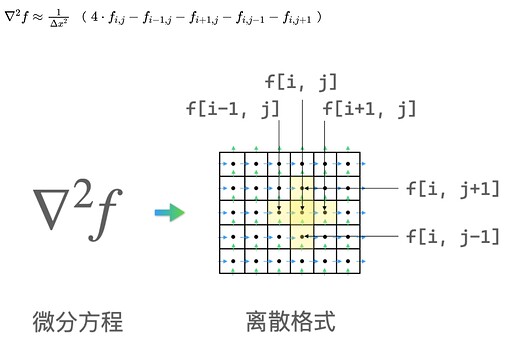
在求解步骤中,首先我们往往需要将描述流场流动的方程——纳维-斯托克斯(Navier-Stokes)方程中的微分项进行离散化处理,用离散数值的代数多项式来近似微分项。比如对一个标量施加拉普拉斯算子的运算往往可以用网格上五点的离散格式来近似:
接下来,我们需要将离散化的方程进行求解。此时,我们面对的往往是一个𝐴𝑥=𝑏 的线性系统,根据矩阵的大小和稠密程度,我们可以选择直接求解法或者迭代求解法来求得未知向量 𝑥。这里我们注意到,**不论是微分项的离散,还是线性系统的求解,往往包含了对目标场上大量元素执行类似且互相独立的计算操作:这种运算模式是非常适合并行加速的。**后面我们会具体看看在代码中怎么用 Taichi 来实现这种加速。
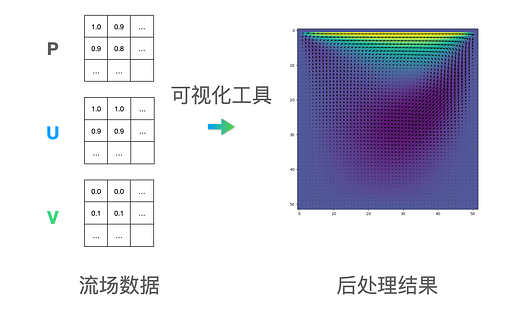
最后,在后处理中,我们需要将前面求得的流场数据进行可视化处理,变成更加易于读取的矢量图,梯度图等等。比如,下图是一个将顶盖驱动流的流场中速度矢量用 Matplotlib 进行可视化的例子。这个部分可视化的工作既可以利用 Taichi 自带的 GUI 完成,也可以根据需要借助一些现有的其他可视化工具。
至此,整个流场的计算过程就完成了,下面我们来看看这些步骤是否都可以在 Taichi 中实现。
02 Taichi 语言是否能应对流体计算的需求
Taichi 作为图形学研究的工具而诞生,使得其天生就具备了很多为大规模数值计算准备的数据结构和并行运算加速机制。同时,作为一门内嵌在 Python 中的领域特定语言(DSL),你可以直接用 Python 来处理不需要高性能并行计算的部分,而把 Taichi 专门用在需要大量并行运算的代码上。
用 Taichi 来加速流场求解中需要大规模并行运算的部分
我们再次以上面的欧拉视角流体算法为例。
数据结构
为了让 Taichi 将求解部分的计算进行并行化处理,我们需要将流场数据保存成 Taichi 提供的 field 的形式。对于流体计算中经常出现的标量场和向量场,Taichi 都提供了对应的数据结构。比如一个 640x480 的由浮点数组成的标量场可以表示为:
f_2d = ti.field(float, shape=(640, 480))
类似的,一个 640x480 的 2 维向量场可以表示为:
v_2d = ti.Vector.field(n=2, dtype=float, shape=(640, 480))
除此之外,Taichi 中还提供了 Matrix 场以及自定义 Struct 场等更多丰富的数据结构,有兴趣的读者可以参阅官方文档的 field 的相关部分。
并行加速机制
假设我们要计算上面的 f_2d 这个标量场印加拉普拉斯算子的结果,我们可以先申请一个用来保存结果的场:
f_2d_grad2 = ti.field(float, shape=(640, 480))
然后我们需要遍历 f_2d_grad2 中的元素,计算其在施加了拉普拉斯算子后的值。为了方便地遍历场中的元素,Taichi 提供了好用的 struct-for 语句:
for i,j in f_2d_grad2:
f_2d_grad2[i,j] = 4 * f_2d[i,j] - f_2d[i-1,j] \
- f_2d[i+1,j] - f_2d[i,j-1] - f_2d[i,j+1]
不过上面的 struct-for 语句是 Taichi 的语法,并不能被 Python 处理。为了让 Taichi 来接管并加速这个计算,我们需要把上述计算包裹成一个 Taichi kernel:
@ti.kernel
def fgrad2():
for i,j in f_2d_grad:
f_2d_grad2[i,j] = 4 * f_2d[i,j] - f_2d[i-1,j] \
- f_2d[i+1,j] - f_2d[i,j-1] - f_2d[i,j+1]
这里的装饰器 @ti.kernel 就是所有 Taichi 加速魔法的入口,它的工作可以理解为接收并分析我们的函数代码,并返回一个自动并行化版本的函数:
fgrad2_ti = ti.kernel(fgrad2)
最后当我们调用这个函数的时候,程序就会把控制从 Python 交入 Taichi 手中,并在多个核心上并行执行上述运算,从而达到大大提升计算速度的目的。
数据可视化
Taichi 提供了内建的一个简易 GUI 系统,可以在构建数值计算代码时方便地作为快速检视流场动态的辅助工具。比如说,可以用下面的简单语句来用一个灰度图来可视化上面的 f_2d( gui.set_image 可以接收 Taichi field 或者 Numpy ndarray):
gui = ti.GUI('Title', (640, 480))
while gui.running:
gui.set_image(f_2d)
gui.show()
当然,如果你需要实现比较复杂的后期渲染效果,那么可能需要利用一些其他的后期软件进行动画制作。关于 Taichi 的 GUI 系统是否可以满足你的需求,可以参考官方文档的 GUI 部分。
03 在流体计算中 Taichi kernel 的应用
- 什么样的场景适合使用 @ti.kernel
很多同学对于 @ti.kernel 中的 kernel 这个术语可能有些陌生,其实 kernel 是来自于 GPU 运算的一个名词,其含义是被运行在 GPU 的计算核心上的运算代码。什么样的代码是适合被运行在 GPU 上的呢?往往是那些对大量数据进行重复类似同时又相互独立的计算,比如遍历屏幕上所有像素并对于每个像素点进行色彩计算的代码,图形程序员往往把他们做成一个一个的函数,并指定这样的函数为 kernel,告诉编译器这些函数需要被大量计算核心并行执行。
- 不适合使用 @ti.kernel 的场景
当然并不是所有看上去是循环的计算都是可以做成 kernel 被并行化的。一个经典的例子是斐波那契数列的计算:由于每个后续数字的计算都是依赖于前面的结果的,这样的计算往往不适合被并行执行。放到计算流体力学中,不同时间层次间的推进由于需要依赖上个时间步的结果,也是不能被并行的,而每个时间层次在同一迭代层面上的计算则往往是可以被并行的。这部分 kernel 的应用区分我们也会在后续的计算流体相关博客中继续结合实例说明。
04 小结
我们回顾并思考了数值流体计算的核心需求,其中计算量最大的往往是对 2 维或者 3 维数组进行的操作,而 Taichi 提供的并行加速机制非常适合用在此类的计算上,因此 Taichi 完全可以用来做 CFD 相关的代码开发。作为社区活动的一环,我们拟定展开流体数值计算 SIG(Special Interest Group)的活动,帮助大家一起学习交流使用 Taichi 进行 CFD 项目编写,现正在邀请社区成员填写问卷调查并加入群组,请有兴趣的同学不要错过!(扫下方二维码即可填写问卷)

下期预告:用 Taichi 语言能获得多大的性能提升?
在文末,我们说到了将大规模运算从 Python 交入 Taichi 手中就可以方便地在多核心上执行,并大大提高运算速度。但是「大大提高」究竟是提高多少呢?在下一篇博客中,我们将初探用 Taichi 能够获得多大的性能提升。