哇,这个投稿好棒呀!!
来报个到![]() ,和彭老师合作特别顺利!短短半个月时间就做出了这样一个有趣的demo。
,和彭老师合作特别顺利!短短半个月时间就做出了这样一个有趣的demo。
是22天 (纠正)
确实,按照你补充的网格信息,原文档是说的通的。
更改和补充Demo:
斯坦福兔子自由落体撞击水平表面
本例展示了一个斯坦福兔子形状的胶结团块自由落体撞击水平表面,然后破碎的过程。本例可用于大规模体系仿真的性能测试。

柔软的斯坦福兔子自由落体撞击水平表面
本例展示了一个斯坦福兔子形状的胶结团块自由落体撞击水平表面的过程。由于胶结强度极高,兔子不会破碎;相反,由于胶结弹性模量相对较低,兔子会表现出相当软的力学响应。本例可作为上例很好的对比。

因Taichi论坛上传图片大小限制,上述Demo GIF效果欠佳。请前往GitHub代码仓库查阅高清GIF (地址详见原帖)。
最后几天截止时间我也来加一点:
- 实现了三维离散元的linear contact model/HM model/linear rolling contact model
- 并加入了库伦摩擦定律以及rolling、twisting的计算,使得球形颗粒能做出非球形颗粒的效果
- 采用verlet table减少neighbor contact list的更新次数
- 用两个field写了一个简单的hash table来做切向力的积分,减少哈希冲突
- 利用taichi写了几个简单的四元数函数,完整地考虑了颗粒的旋转与方位
附上我的源码以及动画:
这是不加rolling的自然休止角

由于文件大小限制,加了rolling和twsiting之后的自然休止角动图请移步
并且通过计算几个案例的计算,验证了代码的可靠性。
压线来投个稿。我尝试改进原有方法在出现大粒子的情况下无法使用小网格的问题。改进后的方法能在有大粒子存在时依然使用较小的网格,只不过这样做性能的提升并不高,不知道有没有更好的处理方法。方法阐述详见github README。
Github repo: GitHub - DesmondZhong/dem
动图

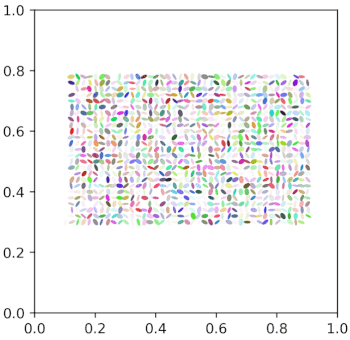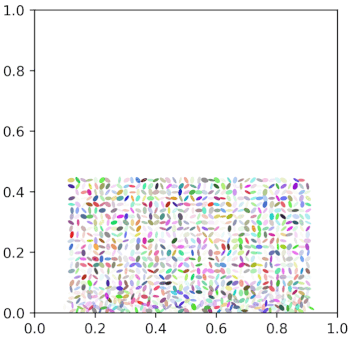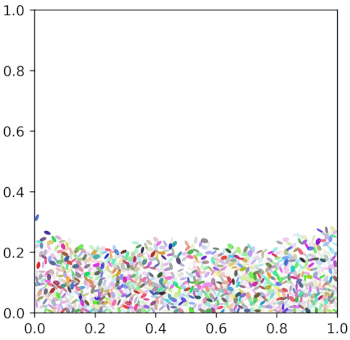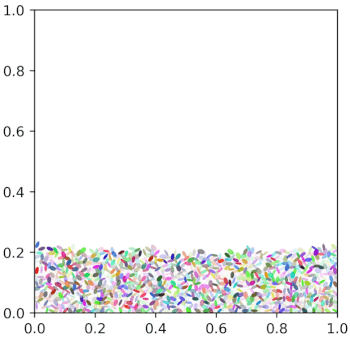
新手小白也来压线投个稿,本意是想把圆形离散元扩展到椭圆形,奈何在椭圆形接触判断这块问题太大,目前只是基于圆形颗粒初步地实现了椭圆形颗粒的可视化,之后多向各位大佬请教。
Github repo: GitHub - JieQi-github/taichi_dem_ellipse_visualization: ellipse visualization based on taichi_dem
GIF:
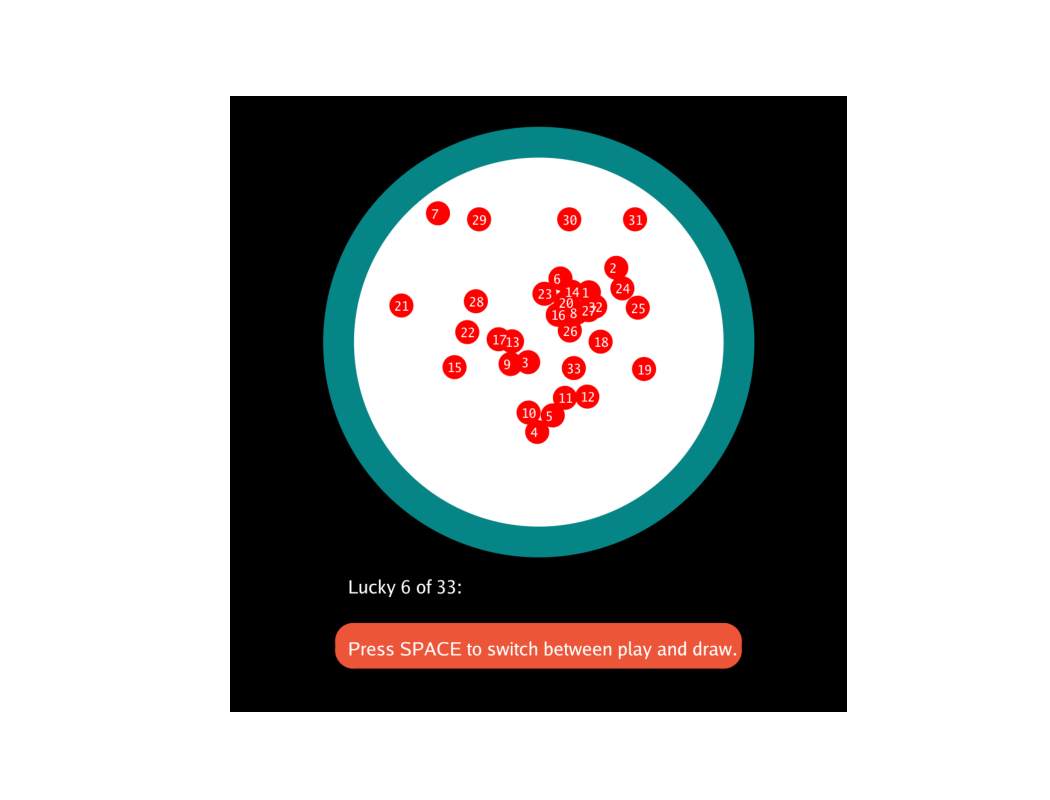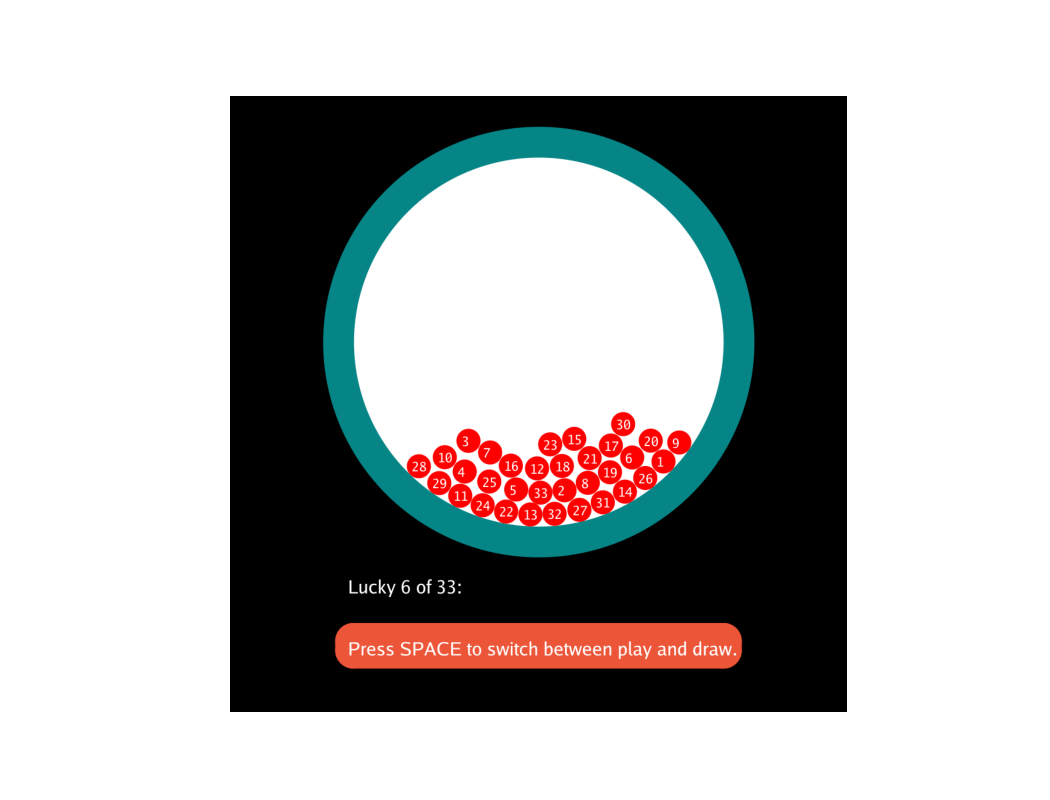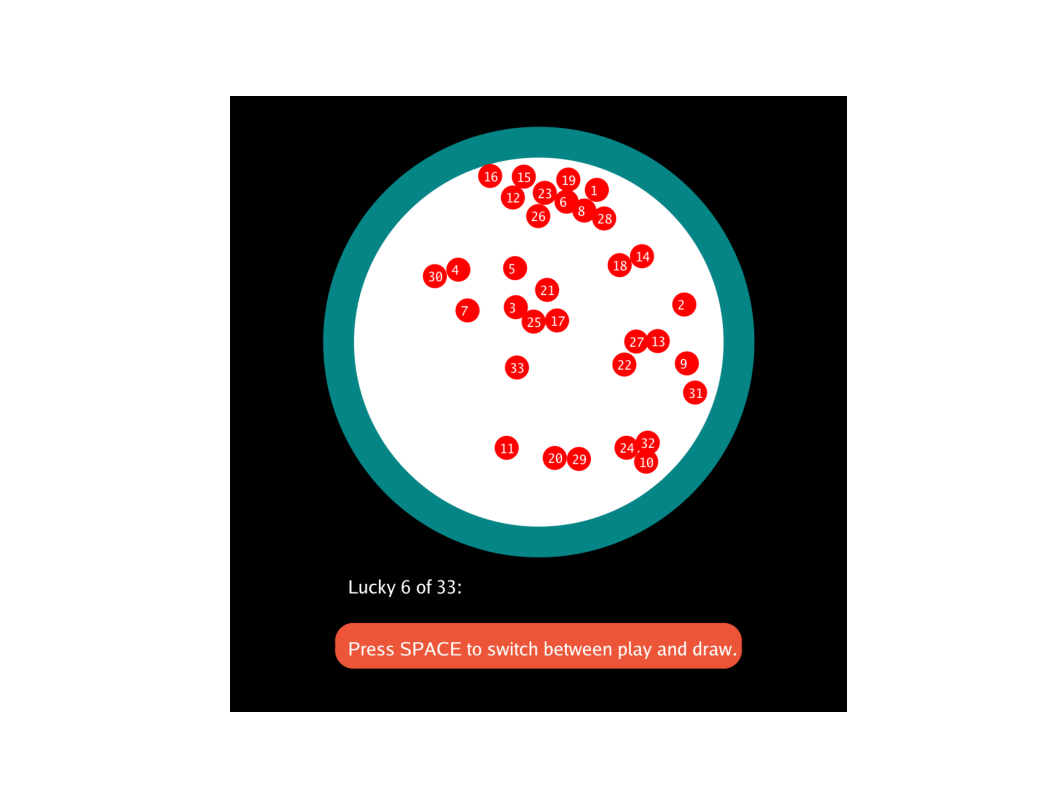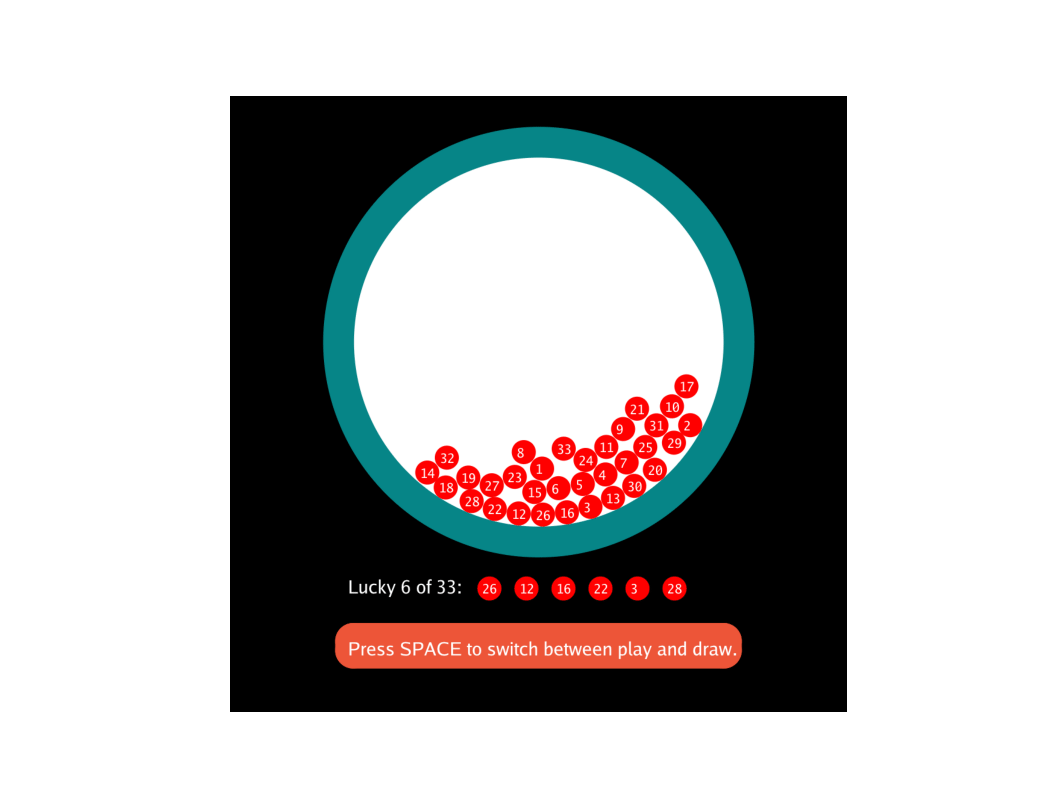
向各位大佬学习,模拟下福彩双色球红号"33选6",玩(play)时球随机跑,抽奖(draw)时球自由落体,速度较小时,最下边6个为中奖号码
Githup repo: GitHub - sanlishi/lottery_sim
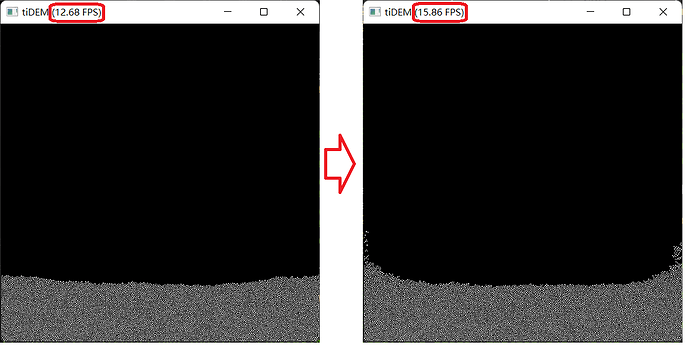
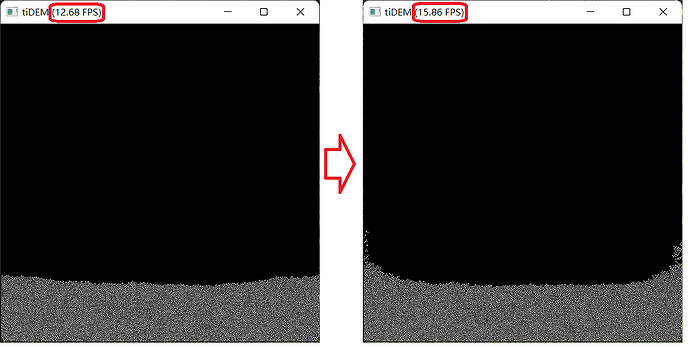
优化内容:
1:list的内存排布。
2:增加gf2,保存粒子id 改为 保存粒子数据。
本地测评:从12.4FPS 优化到 15.1FPS(参数相同的情况下测试)
dem.py 修改后的代码
dem_v0.py 同参数的原始代码
请问你修改过后的list排布里grid_sp=8这个参数一般取多少能最大化的优化性能呢,跟每一维度的网格数有关嘛
![]() DEM 代码优化挑战赛目前已经截止投稿了~ 感谢以下几位投稿选手:@llinus、@ mrzhuzhe、@ Mugi、@ Denver_Pilphis @ MuGdxy、@ Otis、@ DesmondZhong、 @JieQi-github、@ sanli、@ kphmd
DEM 代码优化挑战赛目前已经截止投稿了~ 感谢以下几位投稿选手:@llinus、@ mrzhuzhe、@ Mugi、@ Denver_Pilphis @ MuGdxy、@ Otis、@ DesmondZhong、 @JieQi-github、@ sanli、@ kphmd
代码评审&投票时间:10/31-11/4
敬请期待!
可以编辑一下你的回复,增加一张效果图~
![]() 投票通道已开启!大家可以为自己喜欢的作品投票了~
投票通道已开启!大家可以为自己喜欢的作品投票了~
投票时间:10/31-11/4