请问关于mpm88的fx和base到底代表什么？

嗯嗯，这是一个很好的问题，确实很容易让你迷惑。
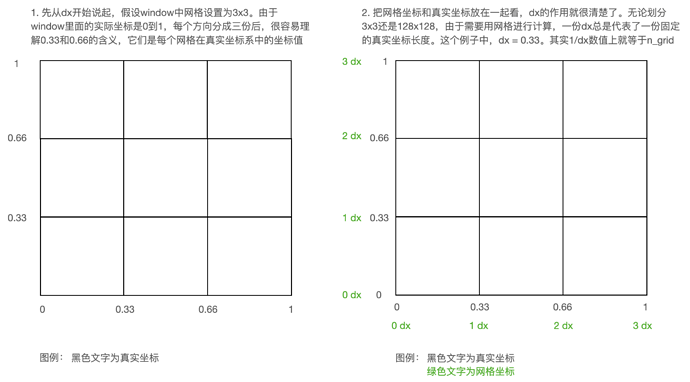
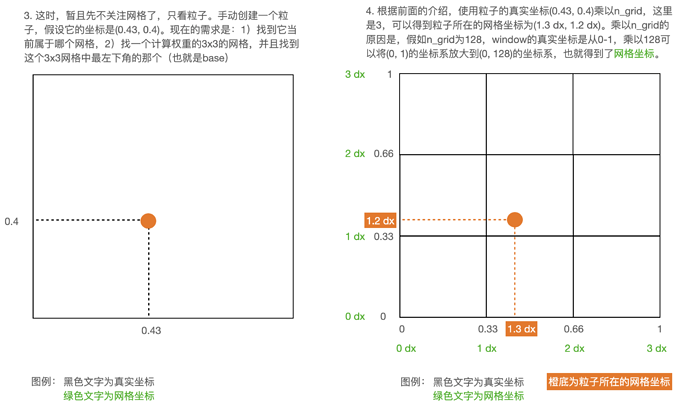
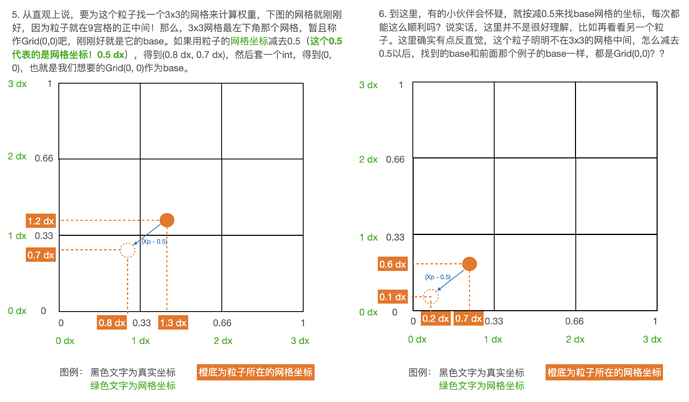
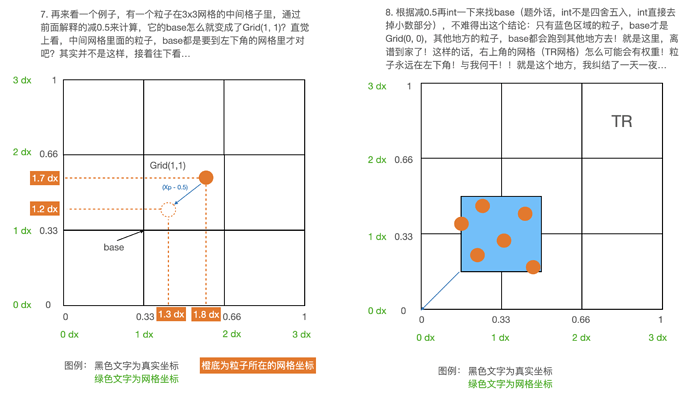
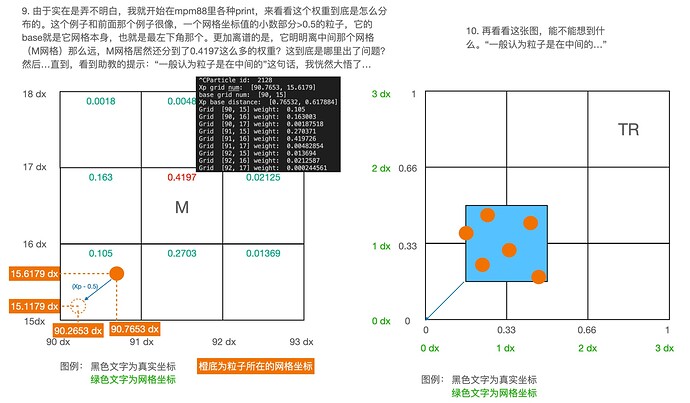
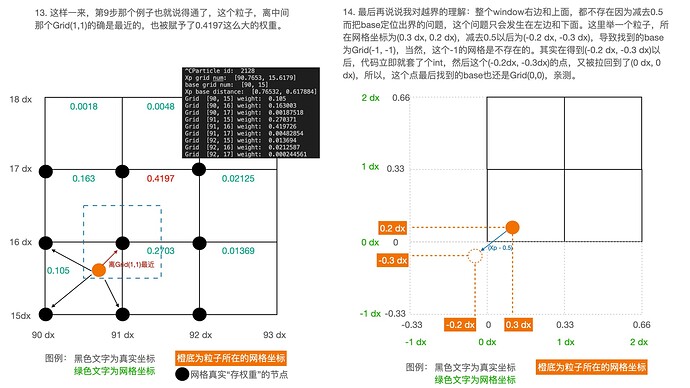
首先，减去0.5的原因是我们一般认为粒子在网格的中间。胡老师在Games 201, Lec 7, page 16，讲过为什么减去0.5，可以在B站具体听一下讲解here。

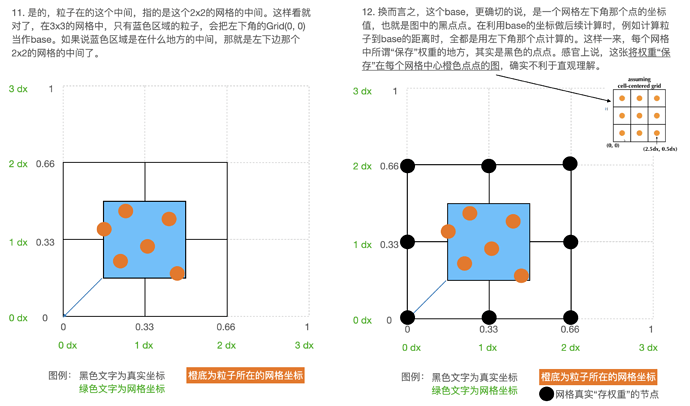
MPM中P2G阶段，需要将particle上的信息按照权重 w ，分散到周围的网格点上，这个例子里面就是 3\times3 的网格大小。
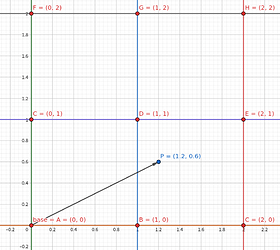
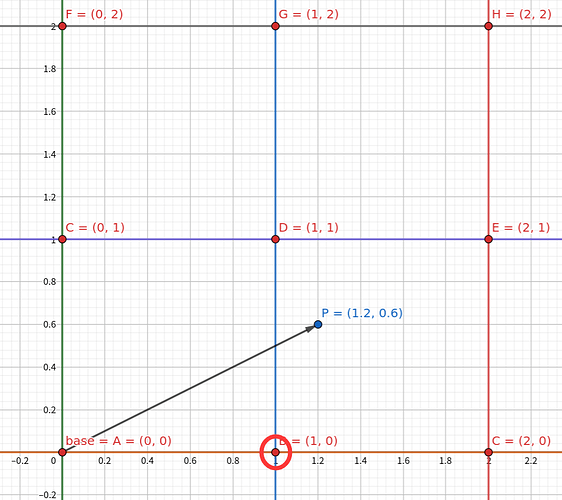
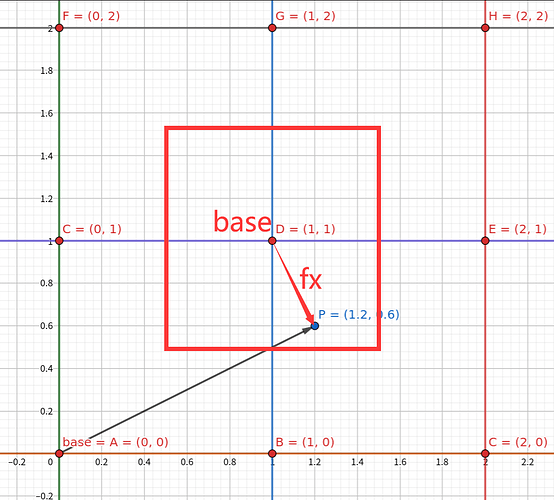
base 就是 这个网格的左下角网格点的位置。fx就是particle 到base网格点的差值。

我们可以以 p=[1.2,0.6], dx = 1.0 为例，研究一下权重 w 的求解。

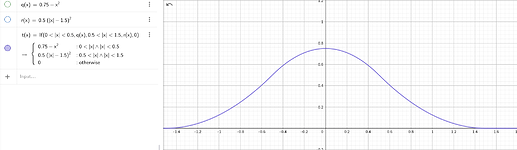
我们这个例子中使用的是Quadratic kernels

那么 p 在 x 轴上，根据距离差可以算出和对应网格顶点的权重
对base的影响（权重 w ）应该是 N(1.2)
对B的影响（权重 w ）应该是 N(0.2)
对C的影响（权重 w ）应该是 N(-0.8)

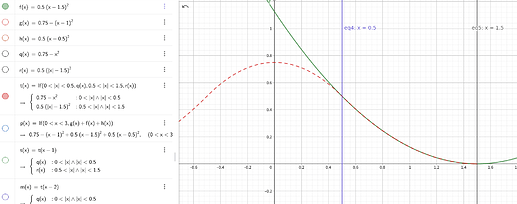
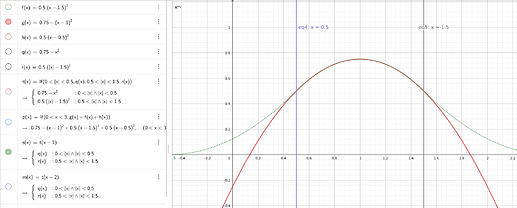
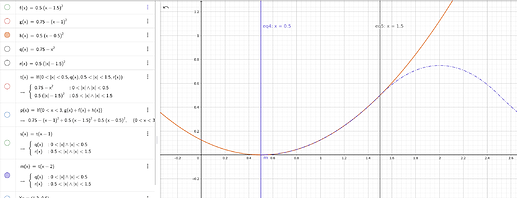
你现在应该都还是很清楚的，但是你会看到这个公式和代码中的公式是不一样的。这就要涉及到一些数学了。我们将核函数 N 根据定义域分为三个部分 [-1.5, -0.5], [-0.5, 0.5], [0.5,1.5] 。这三个部分都可以用 [0.5,1.5] 的三个函数来表示。依然用图片给你展示一下：

1. N(x) \in [0.5,1.5] = f(x) \in [0.5,1.5]
   

   

   image1998×791 135 KB

2. N(x) \in [-0.5,0.5] = g(x) \in [0.5,1.5]
   

   

   image2119×856 164 KB

3. N(x) \in [-1.5,-0.5] = h(x) \in [0.5,1.5]
   

   

   image2265×871 164 KB

综上，你可以看出来
对base的影响（权重 w ）应该是 N(1.2), 也就是 f(1.2)
对B的影响（权重 w ）应该是 N(0.2), 也就是 g(1.2)
对C的影响（权重 w ）应该是 N(-0.8) ， 也就是 h(1.2)
其中 1.2 = fx.x ，
那么 mpm88.py的Line 37

w = [0.5 * (1.5 - fx)**2, 0.75 - (fx - 1)**2, 0.5 * (fx - 0.5)**2]

中的 w[0].x = f(1.2) = N(1.2), w[1].x = g(1.2) = N(0.2) , w[2].x = h(1.2) = N(-0.8) 。

Y轴同理 w[0].y = f(0.6)=N(0.6), w[1].y = g(0.6)=N(-0.4), w[2].y = h(0.6) = N(-1.4)

过这么久了，自己动手写了一下SPH，我总算是明白为什么会减去0.5了。

不知道我想的对不对，如果不对请指正。

这是因为粒子在右边界和上边界计算出的网格编号会溢出，减去0.5相当于把整张网格向左下方平移了0.5个单位。

为什么会溢出，是这样的：
假设整个计算区域大小是100x100， 网格尺寸是1x1

我们利用int()来向下取整，假如粒子在上边界，比如position=（50，100），那么，当粒子的y坐标100转换为网格ID的时候，由于是向下取整的，网格的y编号就会变为100，但是网格的y编号的范围是0~99(因为从0开始算100个网格)。这就导致计算的网格编号超出范围了！

有边界也是同理的。

假如不是恰好在边界，而是稍微超过边界，比如100.1，那也会造成溢出。

但是下边界和左边界就没事，因为-0.1取整之后还是0，没有超出范围。所以左下边界是本身就具有一个单位的裕量的。

解决方案就是把整个网格整体向左下平移0.5个单位。这样原本100.1也会变成99.6，取整之后变为99，不会超出范围。移动之后，上下左右四个边界都拥有了半个单位的裕量。

同时，还应该注意边界处理的时候，把超过边界的值挪动到离着边界还有一个裕量的位置，而不是恰好在边界上，比如100-eps，eps可以设置为0.1

同时，最好给边界多预留一些距离，比如MPM99里面处理边界的时候，就在离着边界的距离小于3个单位的时候，就假设它穿过了边界，然后处理。

感谢解答，对于理解代码很有用。

当0.5<=x<1.5, base node 为0
当1.5<=1.5<2.5, base node 为1
…

但是我有一个疑问, 当粒子 x<0.5时，base node 依然为0，但是weight的计算（w = [0.5 * (1.5 - fx)**2, 0.75 - (fx - 1)**2, 0.5 * (fx - 0.5)**2]）并不适用，对于这些粒子，怎么处理？

Hi @xiangzi , 应该还是适用的。你可以跟着代码和公式过一遍。即使base node 还是0， 也还是可以以base node 为原点，遍历3x3的网格顶点，而对应的weight计算公式还是不变。

假设找到一个粒子，使得fx=0.1, base node 是0， 那么把fx代入w计算得到的weight是=[0.98, -0.06, 0.08], 这是不合理的，是我哪里理解错了吗

请问，计算出来的fx在x方向是fx.x=1.2，然后带入w；但为什么y方向的fx.y却是不一样的值f(0.6),g(1.2),h(1.2)；以x的f(x),g(x),h(x)来计算，在计算出来的y方向的不应该是fx.y=0.6,f(0.6),g(0.6),h(0.6)这样吗？

系统梳理了一遍原理~如有不严谨的地方请多指教

/(ㄒoㄒ)/~~不让俺上传多张图片，那就只能传到B站上了

https://www.bilibili.com/read/cv16719283

原理与程序部分：

例子：
https://www.bilibili.com/read/cv16719283

同学，谢谢你。我仔细看看！

谢谢指出错误，已经更改了。

大佬您好，我带了几个点检验了一下胡老师代码(pic_vs_apic.py)里计算base的方法，得到的结果似乎是B点（借用一下您的图）

当dx等于网格维度的倒数的时候，好像base是当前位置左下角的网格点。这里有点没搞明白。。。
于是我按照自己的理解写了一个计算base的方法。base是距离该位置最近的网格点，然后以base为中心计算9个点的权重，最后完成P2G和G2P操作。如图所示，红框是以D点为中心的网格，在红框范围内的粒子计算出来的base就是D点。

代码如下：

@ti.kernel
def my_PIC():
    for p in x:
        # 胡老师的算法
        # base = (x[p] * inv_dx - 0.5).cast(int)
        # fx = x[p] * inv_dx - base.cast(float)
        # Quadratic B-spline
        # w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1.0) ** 2, 0.5 * (fx - 0.5) ** 2]
        # 我的理解
        base = ti.round((x[p] * inv_dx - 0.5), int)  # 根据粒子位置计算最近网格位置,以该位置作为中心网格取3*3个网格点分别计算权值
        fx = x[p] * inv_dx - base.cast(float) - 0.5  # 粒子位置-中心网格位置=粒子偏移中心网格的量
        # 以x轴为例，左中右与粒子位置的距离分别为：左=1+fx.x , 中=fx.x , 右=1-fx.x
        # 又因为-0.5<fx.x<0.5，所以0.5<1+fx.x<1.5，0.5<1-fx.x<1.5
        # 所以w计算如下
        w = [0.5 * (0.5 - fx) ** 2, 0.75 - fx ** 2, 0.5 * (0.5 + fx) ** 2]
        for i in ti.static(range(3)):
            for j in ti.static(range(3)):
                # offset = ti.Vector([i, j]) # 胡老师的算法
                offset = ti.Vector([i - 1, j - 1])  # 我的理解：因为base是中心点，所以他的左下邻居的偏移量应该是[-1,-1]
                weight = w[i][0] * w[j][1]
                grid_v[base + offset] += weight * v[p]
                grid_m[base + offset] += weight

    for i, j in grid_m:
        if grid_m[i, j] > 0:
            inv_m = 1 / grid_m[i, j]
            grid_v[i, j] = inv_m * grid_v[i, j]

    for p in x:
        # base = (x[p] * inv_dx - 0.5).cast(int)
        # fx = x[p] * inv_dx - base.cast(float)
        # Quadratic B-spline
        # w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1.0) ** 2, 0.5 * (fx - 0.5) ** 2]
        # 我的理解
        base = ti.round((x[p] * inv_dx - 0.5), int)  # 根据粒子位置计算最近网格位置,以该位置作为中心网格取3*3个网格点分别计算权值
        fx = x[p] * inv_dx - base.cast(float) - 0.5  # 粒子位置-网格中心位置=粒子偏移中心网格的量
        w = [0.5 * (0.5 - fx) ** 2, 0.75 - fx ** 2, 0.5 * (0.5 + fx) ** 2]
        new_v = ti.Vector.zero(ti.f32, 2)
        for i in ti.static(range(3)):
            for j in ti.static(range(3)):
                weight = w[i][0] * w[j][1]
                # new_v += weight * grid_v[base + ti.Vector([i, j])] # 胡老师的算法
                new_v += weight * grid_v[base + ti.Vector([i - 1, j - 1])]  # 我的理解：因为base是中心点，所以他的左下邻居的偏移量应该是[-1,-1]

        x[p] = clamp_pos(x[p] + v[p] * dt)
        v[p] = new_v

效果看起来和胡老师的代码是一样的。
我有两个疑问：
1.我的理解到底对不对。
2.如果我的理解是对的，那么我的方法和胡老师的方法在效率上哪个更好一点。
感谢大佬解惑！

base 点的坐标，你可以在python里跑一下看看

base.x = int(1.2 - 0.5) = int(0.7)  = 0
base.y = int(0.6 - 0.5) = int(0.1)  = 0

减0.5和的问题我也困扰了好久，貌似想通了，做了下记录。
不知道我这个理解对不对。。。求证实

非常详细的解释哈，确实如你所说，是在黑色格点上计算权重的。

您好 请问 在flip 中为何一般都是在x y z 三个方向上为何是用 4X3X3 而不是 3X3X3来算权重？

@ti.func
def interp_grid(base, frac, vp):
    
    # Index on sides
    #idx_side = ti.Vector([base-1, base, base+1, base+2])
    idx_side = [base-1, base, base+1, base+2]

    # Weight on sides
    #w_side = ti.Vector([quadratic_kernel(1.0+frac), quadratic_kernel(frac), quadratic_kernel(1.0-frac), quadratic_kernel(2.0-frac)])
    w_side = [quadratic_kernel(1.0+frac), quadratic_kernel(frac), quadratic_kernel(1.0-frac), quadratic_kernel(2.0-frac)]
    
    # Index on center 
    #idx_center = ti.Vector([base-1, base, base+1])
    idx_center = [base-1, base, base+1]

    # weight on center 
    #w_center= ti.Vector([quadratic_kernel(0.5+frac), quadratic_kernel(ti.abs(0.5-frac)), quadratic_kernel(ti.abs(0.5-frac)), quadratic_kernel(1.5-frac)])
    w_center= [quadratic_kernel(0.5+frac), quadratic_kernel(ti.abs(0.5-frac)), quadratic_kernel(1.5-frac)]

    #for i, j, k in ti.ndrange(4, 3, 3):
    for i in ti.static(range(4)):
        for j in ti.static(range(3)):
            for k in ti.static(range(3)):
                w = w_side[i].x * w_center[j].y * w_center[k].z
                idx = (idx_side[i].x, idx_center[j].y, idx_center[k].z)
                grid_v_x[idx] += vp.x * w
                grid_w_x[idx] += w
        

    #for i, j, k in ti.ndrange(3, 4, 3):
    for i in ti.static(range(3)):
        for j in ti.static(range(4)):
            for k in ti.static(range(3)):
                w = w_center[i].x * w_side[j].y * w_center[k].z
                idx = (idx_center[i].x, idx_side[j].y, idx_center[k].z)
                grid_v_y[idx] += vp.y *w
                grid_w_y[idx] += w

    #for i, j, k in ti.ndrange(3, 3, 4):
    for i in ti.static(range(3)):
        for j in ti.static(range(3)):
            for k in ti.static(range(4)):
                w = w_center[i].x * w_center[j].y * w_side[k].z
                idx = (idx_center[i].x, idx_center[j].y, idx_side[k].z)
                grid_v_z[idx] += vp.z * w
                grid_w_z[idx] += w

代码文件：Reisen/3d_pic.py at main · mrzhuzhe/Reisen · GitHub

这个很简单，你只要在P2G和P2G这两个部分，根据particle位置计算grid index的时候考虑grid的平移就可以了。

其实[3,3,3]也是可以的吧。

您好，请问您这个图是用什么软件画的呀？

感觉这个代码的确对初学者来说不太友好，容易造成混乱：
（1）这里减去0.5其实与cell的中心点没有关系，只是求3×3网格节点左下角点的一个trick，每个粒子（particle）取的base节点使得粒子的fx（相对坐标）为0.5≤fx<1.5，粒子位于以3×3的中间节点为中心的单位正方形内，这样中间节点和两侧节点对应的w公式是固定的。
（2）背景网格求质量还是权重都是在网格节点上的，而不是在中心点上的，w的3元素公式对应的坐标分别是0,1,2也说明了这点。
（3）Xp<0.5的情况w计算是不对的，但是mpm88的边界三层节点是固定的，所以没有影响，因此粒子也不会跑到边界cell上去。

如果上述叙述没有问题的话：
（4）在用offset时，右侧和上侧是会越界的，也是bound是三层，粒子不会跑到最边界的cell中去。
（5）速度和质量都在网格节点上（不是cell的中点）的话，dx=1/(n_grid-1)才是合理的。

虽然这些不影响计算结果，可是给学习带来了很大困惑。

非常感谢你的解答，这里我还是有一个小问题：在mpm代码中， inv_dx =float(n_grid)，也就是说黑色节点中间线段的数量是n_grid，那么黑色节点的数量应当是（n_grid+1，n_grid+1），但是在代码后续的定义中grid_v = ti.Vector.field(2, dtype=float, shape=(n_grid, n_grid))，这样最右一列和最上一列节点就不会被遍历到了吧？